Contexto da prática profissional

Na formação de educadores e professores para os anos iniciais do Ensino Básico (EB) há estudantes, futuros professores do EB, que manifestam uma relação difícil com a matemática (Fonseca & Cunha, 2012): revelam conhecimentos reduzidos, dificuldades em lidar com os conceitos, falta de confiança nas suas capacidades para enfrentar as questões apresentadas e pouca motivação. O seu afastamento da matemática começou há muitos anos, mas as dificuldades que sentem e a atitude pouco positiva que manifestam corporizam-se como sério obstáculo durante a formação inicial. Em Portugal todos os candidatos a professor do EB necessitam de concluir 30 ECTS em matemática, antes de iniciarem a via profissionalizante, concretizada através de mestrado que confere habilitação profissional para a docência. De entre as diferentes áreas da matemática, a geometria assume, neste contexto, lugar de destaque, já que as palavras de alguns estudantes “Não sou capaz de fazer”, “Detesto isso”, revelam perceções que a formação inicial de professores deve esforçar-se por ajudar a ultrapassar.

A geometria é uma área importante para trabalhar com as crianças dos anos iniciais (crianças dos 3 aos 12 anos), já que percecionam o mundo através dos sentidos, precisam descobrir, identificar e distinguir formas, de se posicionar e orientar relativamente a elas. Os estudantes precisam de compreender conceitos, aplicá-los para resolver problemas e avaliar a adequação das respostas obtidas ao contexto inicial (Schleicher, 2012). Precisam de perceber que os conceitos estudados, apesar de muito antigos, têm aplicação no dia a dia e não são apenas assuntos académicos. Esta premência é tanto mais significativa quanto menor for a idade das crianças com que estes estudantes, futuros professores do EB irão trabalhar. A formação inicial de professores precisa influenciar o modo como os estudantes desenvolvem os seus conhecimentos, capacidades e atitudes para que no futuro possam influenciar positivamente as suas práticas como educadores e professores e produzir mudanças no modo como as crianças se envolvem com a matemática, particularmente com a geometria (Blanco & Barrantes, 2003).

Envolver e motivar os estudantes, futuros professores, para o trabalho com a geometria é desafio que nos preocupa como formadoras de professores e que urge ultrapassar. Como Maehr e Meyer (1997) expressaram, a motivação é a condição sine qua non para a aprendizagem. Potencia a utilização de recursos para aprender, a persistência, a manutenção do esforço, o entusiasmo e aumenta a confiança nas capacidades para superar tarefas (Eccles, Wigfield & Schiefele, 1998).

Como agir na formação inicial de professores, numa unidade curricular de Geometria, no curso de licenciatura em Educação Básica? Que propostas apresentar? Que desafios colocar? Pretendia-se envolver ativamente os estudantes em tarefas que lhes permitissem aumentar os seus conhecimentos, compreender conceitos geométricos e perceber a sua aplicabilidade, diminuir as suas dificuldades, aumentar a sua confiança nas próprias capacidades, mas também desafiá-los a ser criativos e desenvolver a sua motivação para a aprendizagem da geometria.

Na nossa vida do dia a dia estamos rodeados por objetos geométricos naturais ou construídos pelo ser humano. Algumas embalagens para comercialização de produtos variados são interessantes do ponto de vista geométrico. Pequenas ou grandes, simples ou complexas, sóbrias ou exuberantes, estampadas ou de apenas uma cor. Apelativas e agradáveis à vista. Poderão ser melhoradas? Poderão reduzir a pegada ecológica que realmente vão deixando pelo planeta?

Uma ideia começou a tomar forma.

Um projeto.

O projeto teve início no ano letivo 2010/2011 e terminou no ano letivo 2014/2015, contando com 408 participantes. Em cada ano letivo o projeto desenvolveu-se de fevereiro a maio.

Em 2010/2011 propôs-se aos estudantes que, em grupo, criassem uma nova embalagem para um produto. Colocaram-se algumas questões: Que produto? O mesmo produto para todos? Produtos diferentes? Decidimo-nos por um mesmo produto para todos e a sua escolha revelou-se fácil: embalagem para cápsulas de café. Que cápsulas? Delta Q. Porquê? Eram as cápsulas que podíamos disponibilizar, em grande número, aos estudantes para o desenvolvimento do projeto.

Relato da prática profissional

A solicitação do projeto formalizou-se com um guião onde constava a especificação do pedido:

• Pretende-se que cada grupo (4 ou 5 estudantes) construa uma embalagem para cápsulas de café Delta Q.

• A caixa deve ser inovadora, criativa e uma mais-valia para a empresa e para o comprador. Podem alterar o número de cápsulas, podem propor a venda de vários tipos de café na mesma caixa, podem propor …

• O grupo deve pensar nos argumentos a usar para “convencer” a empresa Delta Cafés a comercializar a nova embalagem. Questões ecológicas, económicas e de reutilização devem ser tidas em conta.

• Devem consultar o site da empresa para se inteirarem dos tipos de café comercializados, e do formato das embalagens. 

Foi solicitada a construção de um protótipo da nova embalagem com dimensões reais (escala 1:1), a depender do número de cápsulas a conter e que podia variar em função da proposta, que considerasse aspetos estéticos e criativos; pediu-se a apresentação da sua planificação; os cálculos da área de papel/cartolina gastos para a confeção da nova embalagem; o volume ocupado pela nova caixa; comparação com a embalagem existente, no sentido de evidenciar a adequação da proposta, relativamente à funcionalidade da caixa, tendo em vista a capacidade e economia de custos (gastos em papel e outros materiais).

Os grupos deviam recolher informação detalhada e que considerassem necessária no site da empresa, reunir para um brainstorming, decidir sobre uma ou várias propostas, elaborar um esboço e apresentá-lo às docentes para aprovação, antes do início da execução da proposta. Esta apresentação inicial tinha como objetivo evitar que houvesse muitas embalagens semelhantes, bem como discutir com os estudantes a adequação da sua proposta. O levantamento de questões foi essencial nesta fase, para ajudar os estudantes a refletir sobre as suas ideias. “Não tínhamos pensado nisso” foi expressão muitas vezes ouvida. Estas reuniões repetiam-se até se chegar a uma proposta final.

Para a execução da proposta era permitido aos estudantes agregar colaboradores aos seus projetos, colaboradores estes que os pudessem ajudar em aspetos ligados ao design, à utilização de programas de desenho para a planificação da embalagem (ex. Cad,) e aos materiais a usar na sua construção.

Durante a execução do projeto os estudantes eram apoiados pelas docentes, em regime de tutoria extra aula, no sentido de os ajudar a refletir sobre opções que iam tomando.

O trilho percorrido pelos estudantes para a concretização do projeto (Figura 1) pode sintetizar-se em cinco fases: simpatizar com a ideia do projeto, compreendendo o desafio proposto; precisar e clarificar o problema a resolver, procurando informações e conhecimentos necessários para continuar; idealizar a proposta do grupo; a que se seguiu o prototipar da embalagem para discutir com as docentes e finalmente testar a construção da embalagem definitiva (Bush, Cox & Cook, 2016).

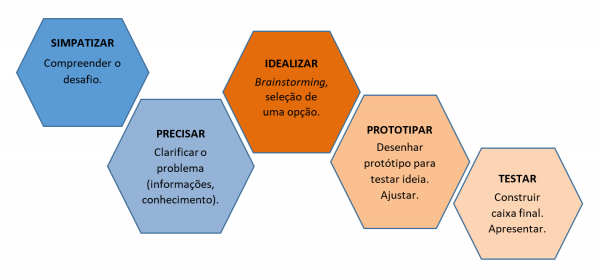
Figura 1: Trilho percorrido pelos estudantes, esquema adaptado de Bush, Cox  e Cook (2016)

Na Figura 2 apresentam-se imagens das propostas da 1.ª edição do projeto (2010/2011).

Figura 2: Embalagens construídas em 2010/2011

As embalagens propostas tinham forma de pirâmide ou prisma, sendo estes convexos ou côncavos. Umas mais funcionais e fáceis de executar, outras mais originais e a necessitar de mais material.

Os argumentos apresentados pelos estudantes para as suas opções prenderam-se com diferentes aspetos:

(a) produzir uma edição reduzida de embalagens, para comemoração de uma data especial da empresa (Figura 3). Esta edição comemorativa poderia revelar-se mais dispendiosa, tanto nos materiais usados como no tempo necessário para a elaboração da caixa, aspetos que do ponto de vista dos estudantes se justificariam;

Figura 3: Proposta de caixa para comemorações especiais

(b) divulgar novos tipos de mistura de café, juntamente com sabores já conhecidos, para analisar a recetividade dos futuros clientes. A cápsula de novo sabor estava visível para o cliente, no centro da caixa, sendo as restantes cápsulas de outro sabor (Figura 4);

Figura 4: Proposta de caixa com uma cápsula surpresa

(c) criar embalagens com vários formatos originais: pentaminó (Figura 5). As caixas poderiam comercializar o mesmo ou vários tipos de café nas diferentes secções e, depois de vazias, serem usadas pelas crianças para, p. ex., construir o puzzle com as doze caixas dos diferentes pentaminós;

Figura 5: Proposta de caixa em formato de pentaminó

(d) criar embalagens que permitissem ao cliente a aquisição de vários tipos (sete) diferentes de café (Figura 6), sem ser necessário comprar a totalidade das cápsulas (setenta) cápsulas, como acontece com as embalagens atuais. Esta possibilidade permitia ao cliente degustar diferentes qualidades de café, com um gasto mais reduzido e com diminuição de gastos de papel da embalagem e consequentemente a redução da pegada ecológica;

Figura 6: Proposta de caixa com sete tios de café

(e) criar embalagens com seis tipos de café diferentes que pudessem ser, simultaneamente, dispensadores das cápsulas (Figura 7);

Figura 7: Proposta de caixa-dispensador com seis tipos de café

(f) embalagens “bonitas e diferentes”, mas facilmente transportáveis “encaixam uma na outra”. O grupo defendia que o efeito estético poderia atrair clientes “nós comprávamos estas embalagens” (Figura 8).

Figura 8: Proposta de caixa côncava

O caminho percorrido até ao produto final foi semeado de obstáculos.

Tal como em qualquer embalagem as dimensões deviam ser adequadas ao produto, nem demasiado grande, nem tão pequeno que dificilmente o contivessem. A medição das cápsulas reais nem sempre foi precisa, como nem sempre foi fácil construir os triângulos, os hexágonos e os octógonos pretendidos. Por outro lado alguns grupos não tiverem em conta a espessura do papel/cartolina com que trabalharam para a proposta final. Com a embalagem concluída detetavam que o número de cápsulas inicialmente pretendido não cabia na caixa. Depois de tanto trabalho era necessário recomeçar! Faziam-no na certeza de um melhor produto. A mobilização e a procura de novos conhecimentos foi uma constante.

Nem todos os grupos planearam o seu trabalho, pormenorizada e atempadamente, aspeto que se refletiu na qualidade do produto final apresentado.

Discussão e avaliação da implementação da prática profissional

As embalagens finais de 2010/2011 (Figura 2) superaram as expectativas iniciais das docentes, pela originalidade e qualidade apresentadas. A criatividade de algumas das propostas entende-se como criatividade coletiva (Yu, Nickerson & Sakamoto, 2012), pois grupos de estudantes envolvidos em tarefa não rotineira e com a cooperação de todos obtiveram um produto emergente. Para os autores a criatividade coletiva baseia-se na natureza da tarefa desenvolvida pelo grupo, rotineira ou não, e na natureza do produto obtido, um produto agregado (ex. Wikipedia) ou emergente. A originalidade das propostas revelou-se pelo facto de serem únicas ou em número muito reduzido, de entre todas as propostas apresentadas (Vale et al., 2012) .

A concretização deste projeto foi um período de aprendizagem também para as docentes. Com o seu desenvolvimento percebeu-se a necessidade de calendarizar pedidos de informação, de modo a suscitar um planeamento mais cuidado e que permitisse aos estudantes obter melhores resultados.

Não foi possível monitorizar todo o processo de preparação das propostas, visto que o projeto foi desenvolvido fundamentalmente pelos grupos fora de sala de aula, apesar de toda a disponibilidade das docentes nos momentos de tutoria. Mas os vários momentos de discussão das propostas, quer com o grupo quer envolvendo vários grupos, contribuíram para a partilha de ideias, a sugestão de soluções para problemas emergentes, vinda por vezes de outros grupos, o desenvolvimento do trabalho em equipa e da comunicação entre todos, como se explicita com a opinião de um aluno.

O desenvolvimento deste trabalho tornou-se um grande desafio. Durante o processo surgiram dificuldades que foram ultrapassadas com as ideias e as capacidades diferentes de todo o grupo (A8)

Como o trabalho era proposto no início do semestre, os estudantes podiam ter necessidade de pesquisar sobre conteúdos geométricos necessários à construção da embalagem. Quando os conceitos eram abordados em sala de aula, alguns dos estudantes participavam de forma mais ativa, de acordo com as suas pesquisas prévias. Os estudantes desenvolveram conhecimentos sobre formas planas, superfícies e sólidos, prismas e pirâmides, planificações, áreas e volumes. A Figura 9 ilustra o planeamento para encaixar no invólucro quatro caixas de cápsulas de café, com formato de prisma triangular regular. A construção do triângulo equilátero partiu do círculo, base da cápsula. Procedendo inicialmente por tentativa e erro para construir o triângulo equilátero, cedo perceberam que aquela não seria a melhor opção. Tiveram de recordar a posição do raio da circunferência e da tangente no ponto de tangência. “Agora percebemos para que serve [o resultado aplicado]. Afinal serve”.

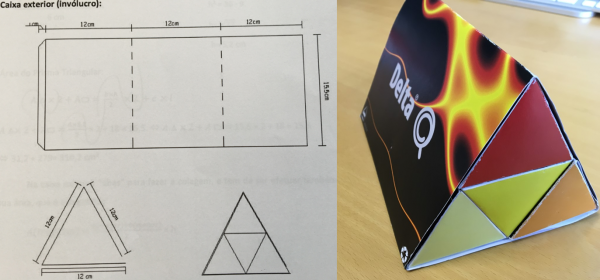
Figura 9: Exemplo de procedimento para a planificação da caixa apresentada

	DELTA_caixa_cafe

A maioria (96%) considerou o projeto como um desafio superado com sucesso, que lhes permitiu desenvolver a criatividade na construção de propostas inovadoras (Aluno 1 – A1), aplicar conhecimentos geométricos (A2 e A3), trabalhar em grupo (A4 e A5), enfrentar as suas capacidades (A6) e aprender a apreciar a geometria (A7).

Este tipo de trabalho é um estímulo à criatividade, iniciativa, capacidade de trabalhar em grupo e ajuda à compreensão da geometria (A1).

Gostei deste projeto! Penso que foi uma vantagem porque pude ser criativo, fazer cálculos, depois construir a caixa com os cálculos, por exemplo, tive a oportunidade de pôr em prática os cálculos que fiz e ver se podia construir uma caixa com eles (A2).

Aplicámos um modo prático e compreendemos que os cálculos são mais importantes do que pensávamos, porque às vezes um pequeno erro estragava a nossa caixa (A3).

Com este trabalho cooperámos e motivámo-nos dentro do grupo, uns puxavam os outros para termos um resultado positivo e obter o nosso objetivo (A4).

Gostei deste desafio. Penso que foi um teste às minhas capacidades porque pensei que no meu grupo não íamos ser capazes de fazer uma caixa. E fomos! (A5)

Um desafio é sempre bom para desenvolver as nossas capacidades e quanto mais difícil melhor. Aprendi que para realizar um projeto é preciso compreender, ter paciência, esforço. São necessárias muitas pesquisas para se atingir o limite das nossas capacidades (A6).

Para mim este trabalho foi importante para aprender a gostar de geometria (A7).

As opiniões da maioria dos estudantes envolvidos foram positivas e a qualidade das embalagens apresentadas permite-nos concluir que o desafio foi adequado aos objetivos iniciais, por ter contribuído para promover conhecimentos e atitudes positivas dos estudantes, face à Geometria.

Como os resultados foram positivos decidiu-se informar a empresa Delta Cafés do projeto. Este aspeto concretizou-se e possibilitou o estabelecimento de um protocolo, entre a empresa e o IPVC, que atribuiu um prémio ao melhor projeto selecionado pela empresa.

O projeto foi desenvolvido em anos subsequentes. Como se pode ver na Tabela 1, em cada ano era proposta uma variante do projeto inicial, desde a alteração da finalidade da caixa até à construção de outros produtos.

Tabela 1: Variantes ao projeto por ano letivo e participantes

Ano Letivo	Caixa para embalar:	Nº de Participantes
2010/2011	Cápsulas de café da Delta Q	104
2011/2012	Biscoitos de canela ou bombons de chocolate negro com recheio de vinho tinto da Adega Mayor	92
2012/2013	Cápsulas de café da Delta Q acompanhada de jogo que envolvesse conceitos geométricos	84
2013/2014	Bombons de chocolate negro com recheio de vinho tinto acompanhada de um voucher para comemorar um dia especial	83
2014/2015	Cápsulas de café da Delta Q	45

Para manter o interesse no desafio aos novos estudantes em 2012/2013 foi-lhes solicitado que incluíssem na proposta a apresentar um desafio para crianças. Enquanto os pais tomavam café as crianças poderiam divertir-se … com a geometria. Na Figura 10 apresenta-se a proposta premiada, que aliou à embalagem o jogo da memória com figuras geométricas.

Figura 10: Proposta de caixa com desafio

No ano seguinte 2013/2014 e para manter o interesse dos estudantes variaram-se as embalagens iniciais da Delta Cafés tendo-se solicitado que criassem uma nova embalagem para os bombons de vinho tinto da Adega Mayor. O desafio foi “grande, porque a embalagem [original] é muito bonita”. No entanto várias foram as propostas e na Figura 11 apresenta-se a proposta ganhadora, que também poderá ser visualizada neste vídeo.

Figura 10: Proposta para caixa de bombons

Os trabalhos finais eram partilhados em grande grupo através de uma apresentação que devia responder às seguintes questões:

• Como surgiu a ideia da caixa?
• Porque escolheram a caixa que apresentaram?
• Que dificuldades tiveram?
• O que aprenderam de Geometria com este trabalho?

No anexo 1 partilha-se uma das apresentações. Note-se que esta apresentação poderá conter imprecisões.