Introdução

As tecnologias sempre estiveram presentes na história do desenvolvimento humano, sendo desde os primórdios um dos principais artifícios para a sobrevivência dos nossos antepassados perante as dificuldades impostas pela própria natureza, além disso, a utilização de tecnologias provoca mudanças em vários aspectos da sociedade, como Miskulin (2010) aborda, as tecnologias da informação e comunicação implicam novas formas de criar, aprender e repassar o conhecimento. Nesse sentido, com a crescente utilização de tecnologias de informação e comunicação, a escola não deveria ficar exclusa, uma vez que é o espaço destinado à formação dos cidadãos, que precisam de conhecimento e preparação para desenvolver-se tanto pessoal quanto profissionalmente.

Programas governamentais, como o Programa Nacional de Tecnologias na Educação (ProInfo), disponibilizam desde 1997 computadores às escolas públicas no Brasil, que podem constituir ferramentas de ensino e aprendizagem se utilizadas adequadamente, sendo recursos para alternativas de ensino diferenciadas, capazes de auxiliar o aluno a desenvolver sua criatividade, capacidade de raciocinar, pensar, argumentar enfim, construir uma postura crítica para tornar-se um cidadão ativo no âmbito social.

No contexto do ensino da Matemática, os computadores em conjunto com os softwares educacionais proporcionam possibilidades como melhor visualização de objetos matemáticos e agilidade em cálculos complexos, favorecendo a melhor compreensão de conceitos matemáticos, podem também ser um meio dos professores utilizarem diferentes alternativas de ensino e, assim, instigar o aluno a raciocinar e participar de forma ativa nas aulas: “As novas tecnologias oferecem instâncias físicas em que a representação passa a ter caráter dinâmico, e isto tem reflexos nos processos cognitivos, particularmente no que diz respeito às concretizações mentais” (Gravina & Santarosa,1998, p.10).

Dada a importância da integração das tecnologias à prática docente, desenvolvemos uma tarefa utilizando o software Br. Office Calc que auxilia no ensino de funções quadráticas. Neste trabalho, apresentamos essa tarefa e o relato de sua aplicação com o objetivo de discutir aspectos pertinentes quanto ao uso das tecnologias digitais no ensino e aprendizagem da Matemática. São evidenciadas as opiniões e visões dos alunos quanto às atividades realizadas, para que assim o professor possa ampliar sua compreensão quanto ao uso das tecnologias digitais para o ensino e aprendizagem da Matemática e se apropriar desta possibilidade de ensino adaptando-a se necessário a sua realidade escolar.

Tecnologias de Informação e Comunicação e Ensino da Matemática

Para formar cidadãos ativos na sociedade, preparados para tomar decisões, formular opiniões e ideias precisamos estimular os alunos a utilizarem seu pensamento crítico, seu raciocínio, sua criatividade, enfim, as capacidades que cada vez mais estão sendo exigidas na contemporaneidade. No contexto do ensino da Matemática é recorrente a utilização da metodologia “tradicional”, pelos professores, em que as aulas são expositivas, ou seja, os alunos recebem o conteúdo matemático e realizam exercícios repetitivos a fim de memorizar algoritmos de resolução.

Numa tal apresentação formal e discursiva, os alunos não se engajam em ações que desafiem suas capacidades cognitivas, sendo-lhes exigido no máximo memorização e repetição, e consequentemente não são autores das construções que dão sentido ao conhecimento matemático (Gravina & Santarosa, 1998, p.1).

 E assim, muitos alunos não vêem sentido em estudar Matemática, consideram as aulas cansativas e não compreendem seus conteúdos, o que pode ser reflexo da metodologia utilizada pelo professor. As tecnologias aliadas às novas alternativas de ensino possibilitam a Matemática ser abordada de forma mais instigante e desafiadora para os estudantes, em particular, os softwares constituem-se ferramentas úteis para o ensino e aprendizagem da Matemática, pois, oferecem dinamismo a aprendizagem de conceitos e propriedades matemáticas, favorecendo a observação e compreensão da Matemática tanto em relação a novos conteúdos quanto aos já estudados.

Entretanto, é preciso ter claro que na educação “[...] a informática não deverá ser vista como redentora [...], mas sim como um elemento a mais a contribuir na construção de uma escola que pode desenvolver mecanismos que contribuam na superação de suas limitações” (Mercado, 2002, p. 133). Então, para que o professor possa realmente utilizar os softwares a favor do ensino e aprendizagem da Matemática “não basta a este profissional dominar apenas o uso da informática educativa. Ele precisa aprender a fazer seu planejamento pautado nas possíveis dificuldades dos alunos com relação ao tema da aula.” (Brandt & Montorfano, 2011, p. 6).

As tecnologias em geral são utilizadas para ampliar as possibilidades de aprendizagem dos alunos, possibilitando pesquisas, melhores visualizações, estímulo do raciocínio e pensamento crítico, mas sozinhas não produzem qualquer efeito, pois é necessário que o professor as utilize em conjunto com metodologias adequadas para explorar ao máximo as possibilidades. E como cita Valente (1997) quanto às competências exigidas dos profissionais no mundo atual, como capacidade de pensar, de aprender a aprender, de trabalhar em grupo.

Certamente, essa nova atitude não é passível de ser transmitida, mas deve ser construída e desenvolvida por cada indivíduo, ou seja, deve ser fruto de um processo educacional em que o aluno vivencie situações que lhe permitam construir e desenvolver essas competências. E o computador pode ser um importante aliado nesse processo (VALENTE, 1997, p. 20).

 Atualmente, a maioria das escolas brasileiras possuem computadores com acesso à internet e softwares educacionais instalados. A utilização de softwares em tarefas planejadas com objetivos específicos possibilita que o aluno teste hipóteses e investigue conteúdos, confira conceitos já estudados, resolva problemas propostos, ou até mesmo de uma forma mais interativa resolva exercícios de fixação. Com a adequada utilização “os softwares são grandes aliados ao desenvolvimento das atividades curriculares, com eles é possível simular situações que facilitam o processo de ensino-aprendizagem” (Bovo, 2004, p. 2).

Tendo em vista que os softwares oportunizam visualização e “manipulação” de elementos que favorecem a compreensão de conceitos matemáticos, acreditamos que os utilizando no ensino da Matemática, o aluno tem maiores possibilidades para generalizar e compreender conceitos matemáticos envolvidos de forma dinâmica e agradável, participando ativamente das aulas de Matemática

Neste trabalho foi utilizado o software Br.Office Calc, que é um software livre pertencente ao pacote do Br.Office. Trata-se de um editor de planilha eletrônica similar ao Excel, do pacote do Office. Segundo Rosa e Viali (2008, p. 185), o Br.Office Calc possibilita ao usuário efetuar cálculos complexos de forma mais rápida com a utilização de fórmulas Matemáticas e funções, livrando o aluno do trabalho algorítmico possibilitando maior tempo para ser dedicado a deduções e conjecturas sobre os resultados obtidos. 

 Organizando o trabalho

Para a realização deste trabalho efetivamos inicialmente pesquisas bibliográficas a respeito da importância do uso efetivo pelos profissionais de ensino, dos recursos tecnológicos no âmbito educacional das instituições de ensino fundamental e médio (em alguns países denomina-se Ensino Secundário) na disciplina de Matemática, também, por meio de pesquisas bibliográficas, estudamos como as tecnologias digitais aliadas às novas alternativas de ensino podem contribuir para o processo de ensino e aprendizagem da Matemática. Com isso, pudemos desenvolver uma proposta para o ensino de funções quadráticas utilizando o software BrOffice Calc, direcionada para alunos do primeiro ano do Ensino Médio, com faixa etária entre 14 e 19 anos.

A proposta de ensino foi aplicada em um colégio brasileiro situado no município de União da Vitória, no estado do Paraná. A escolha do colégio deu-se principalmente por ser um dos três disponíveis na cidade para a realização das atividades de Estágio Curricular Supervisionado, uma etapa obrigatória dos Cursos de Formação de Professores de acordo com as Resoluções CNE/CP[1] nº1/2002 e CNE/CP nº2/2002, e ainda por apresentar em suas dependências um laboratório de informática, assim, a aplicação das tarefas ocorreu em doze horas/aula durante o cumprimento do Estágio Curricular Supervisionado da primeira autora deste artigo.

Descrição da Tarefa Desenvolvida

 A tarefa objetivou compreender o gráfico de uma função do segundo grau como um conjunto de pontos no plano cartesiano e principalmente identificar, por meio de planilha eletrônica, o gráfico de uma função quadrática como sendo uma parábola (uma curva característica).

A partir das respostas dos alunos e da discussão do assunto com o restante da turma ao final de cada tarefa os conceitos foram formalizados.

Roteiro da Tarefa – Estudo dos Gráficos de Funções Quadráticas com o BrOffice Calc

1º) Calcule no caderno, formando uma tabela, 10 pontos da função f(x) = x², escolhendo arbitrariamente os  valores para x no intervalo [-20,20].  (Sugestão escolha valores negativos e positivos).

2º) Abra o software Br.OfficeCalc, perceba que a área de digitação é dividida em retângulos, que formam uma planilha. Cada retângulo recebe o nome de célula, e cada célula está referenciada por uma letra que indica a coluna e um número que indica a linha. Por exemplo, chamamos de A1 a célula localizada na coluna A e na linha 1.

3º) Agora digite, na planilha do Br.OfficeCalc, a tabela que foi obtida a partir da escolha de valores para x, que aplicados na função  f(x) = x² resultam no valor y.

Atenção: digite-os na ordem crescente do valor escolhido para x

4º) Após construir a tabela insira seu gráfico. Para isso, selecione na tabela as linhas e colunas que contém os pontos (x,y) acesse o menu inserir, gráfico, então selecione o gráfico tipo dispersão, pontos.

Observe a dispersão dos pontos escolhidos do gráfico da função f, e elabore um breve relatório.

5º) Construa agora o gráfico da função g(x) = -x² + 2x + 3 através do software Br.Office Calc, na planilha 2, sem calcular os pontos da função no caderno.

6º) Para esboçar o gráfico desta função é preciso saber como calcular os pontos que formam o gráfico de uma função, pois se não souber não conseguirá dar o comando para o computador fornecer o gráfico.

O computador não é pensante não é inteligente, ele simplesmente executa os comandos passados pelo ser humano.

Para obter os pontos da função f você os calculou manualmente depois digitou na tabela para inserir o gráfico.

Agora na função g você digitará, na planilha 2, em formato de tabela de forma crescente os números inteiros do -15 ao 15, ou seja, os valores para o x. Na célula A1 indique a coluna x e na célula B1 indique y Logo abaixo da célula A1, ou seja, na A2 digite -15 e assim por diante, digitando de forma crescente os valores para x

7º) Agora para obter o valor de y, ou seja, o valor da função em determinado ponto, faz-se o computador “tomar conhecimento” da função dando os comandos para que calcule y para os valores de x.

Você sabe a g(x), então sabe que substituindo o x por algum valor, obtém seu correspondente para formar o ponto (x , g(x)), ou simplesmente, (x , y).

No computador representa-se, por exemplo, o valor de x = -15 pela sua localização que neste caso, está na célula A2, além ainda, de utilizar outra simbologia para as operações matemáticas.

Para calcular o ponto no qual x = -15 precisa-se dos coeficientes da função, então na célula D1 digite “a =” e complete a igualdade na célula E1, ou seja, o coeficiente “a” da g(x) que é -1.  E proceda da mesma forma com o coeficiente b e c, nas células D2 e D3.

8º) Agora você sabe a localização dos parâmetros e do primeiro valor de x para efetuar o cálculo do primeiro valor de y. Para isto clique na célula B2, observe que em cima da planilha e embaixo da barra de menus existe um campo de digitação. Nele digitamos as fórmulas, sempre iniciando pelo sinal de igual.

Essa fórmula é a função g(x) = -x² + 2x + 3.

Na qual: a= -1, b= 2 e c= 3.

E queremos aplicar x= -15, então g(-15) = -1.(-15)² + 2.(-15) + 3 = -252.

Ou seja, g(-15) = a.(-15)² + b.(-15) + c

Para calcular no software Br.OfficeCalc, utiliza-se outros símbolos para as operações, exceto soma e subtração, e ainda, ao invés de utilizar diretamente os valores você utiliza sua localização.Vejamos alguns símbolos:

• Multiplicação (x ou), no software é * (asterisco);

• Divisão (÷), no software é / (barra);

• Para elevar ao quadrado utiliza-se ^2( circunflexo 2).

 9º) Para digitar a função g(-15) utilizamos as instruções dadas acima, portanto obtemos = E1*A2²+E2*A2+E3.

10º) Após digitada a função com a aplicação , tecle Enter, então o valor obtido para f(-15) aparece na célula B2. Confira. Repita o processo para encontrar g(x) quando x = -14 e x = -13.

11º) Porém para calcular todos os pontos um por um daria muito trabalho, então façamos com que o computador calcule o valor de y para todos os valores de x.

Clique na célula B4 e na barra de digitação aparecerá a fórmula que está por trás do valor obtido. Observe que os valores de a, b e c são fixos eles fazem parte da lei de formação, então, fixe-os para que apenas o valor de x varie de acordo com a tabela digitada.

Selecione na fórmula da barra de digitação, o parâmetro a, depois de selecionado segure shift e pressione a função 4 do teclado (F4), neste caso aparecerá juntamente à localização de a , que é E1, o símbolo E$1, então este valor está fixado na fórmula. Faça o mesmo para b e c.

12º) Após feito o 11º passo volte para a planilha na célula que permaneceu selecionada B4 e selecione as demais que estão abaixo dela, de um Enter e pronto.  O computador calculou os demais pontos. Para finalizar insira o gráfico.

14º) Agora compare os dois gráficos e relate (em folha para ser entregue e em duplas):

• Semelhanças e diferenças;

• Além da comparação dos gráficos entre si, compare também suas funções e relate as semelhanças e diferenças;

• Responda se é possível definir a forma do gráfico de funções quadráticas;

• Enfim anote todas as observações feitas.

15º) Salve o arquivo. 

	2017-03-01 at 21-53-24

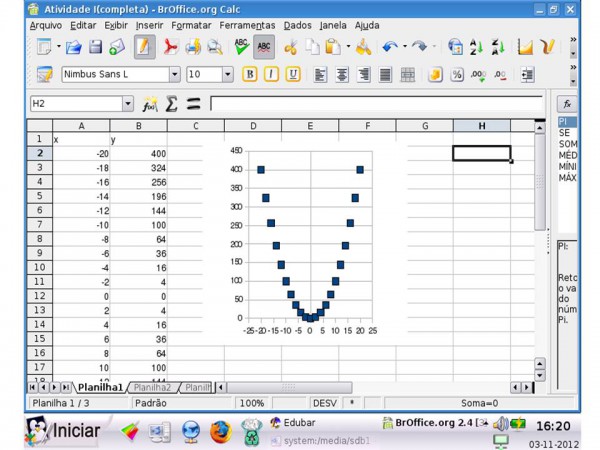
Figura 1 – Visualização do 4º passo do Roteiro da Tarefa. Fonte: Captura de tela do software.

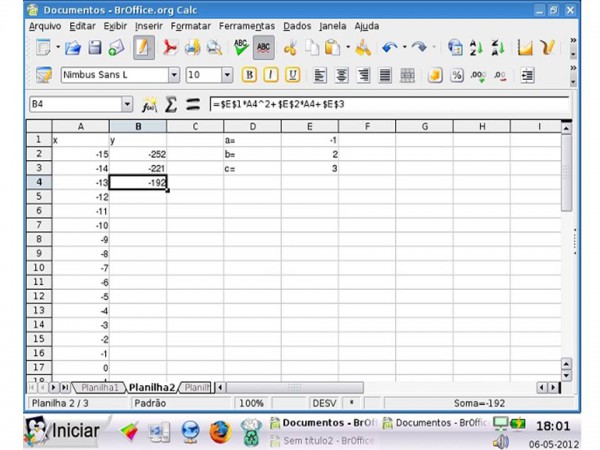
Figura 2 – Visualização do 11º passo do Roteiro da Tarefa.Fonte: Captura de tela do software.

Relato da aplicação da tarefa proposta

Ao iniciar a aula anunciamos aos alunos que as próximas tarefas seriam realizadas no laboratório de informática, o que ocasionou agitação, uma vez que seria uma aula de Matemática “diferente” das tradicionais, por quebrar o paradigma quadro e giz. Assim, a curiosidade e empolgação dos alunos eram evidentes, fatores considerados positivos para a realização da tarefa.

Entretanto, já no laboratório de informática, houve dificuldade de organizar a turma para o inicio da tarefa. Acredita-se que esse tumulto ocorreu pelo fato dos alunos não utilizarem com frequência a sala de informática, tiveram dificuldades em organizarem-se no ambiente do laboratório, também, devido à disponibilidade de poucos computadores e em espaço reduzido, fator negativo para a utilização destes equipamentos na prática pedagógica.

Após conseguir organizar a turma, iniciamos a realização da tarefa em duplas e trios, utilizando um projetor multimídia para auxiliar a ambientar os alunos no software, porém o mesmo não estava bem configurado e acabou limitando a interface do software, neste caso, como havia sido distribuído o roteiro com os passos da tarefa, solicitamos que os estudantes o utilizassem para orientarem-se quanto à realização da tarefa.

No início houve dificuldade por parte da maioria dos alunos com relação ao cálculo, no caderno, dos 10 pontos da função, por isso, aqueles que tinham mais facilidade no cálculo manual se adiantaram, isto contribuiu para que estes se dispersassem em conversas paralelas e com outras ferramentas do computador, o que acabou interferindo de forma negativa no desenvolvimento da tarefa com o restante dos alunos. Estes alunos foram convidados a auxiliar os que não haviam terminado, desta forma minimizamos o tumulto e adiantamos a realização das tarefas.

Depois dos cálculos dos pontos no primeiro passo do roteiro, já com o Br.Office Calc aberto, foram apresentadas algumas considerações quanto à planilha eletrônica. Em seguida, no momento em que deveriam digitar os pontos na planilha uma minoria de alunos se atentou a informação disposta no roteiro quanto à disposição dos valores de x, que deveria estar em ordem crescente, então foi solicitado que reorganizassem a tabela de pontos.

Após todos conseguirem inserir o gráfico (quarto passo do roteiro da tarefa), os alunos se apresentaram muito curiosos, pois queriam comparar os gráficos obtidos com os gráficos dos outros grupos. Houve troca de ideias e comparação entre os resultados para compreender e formalizar suas conjecturas quanto à forma do gráfico da função. Como os pontos plotados no gráfico foram aleatoriamente escolhidos, alguns gráficos não apresentaram uma parábola nitidamente, e como os estudantes ainda não conheciam o formato do gráfico, sentiram dificuldade em reconhecer e comparar o formato gerado pelos pontos, assim, estes começaram a comparar seus gráficos com os dos outros. Neste momento, interferimos alertando-os de que todos construíram o gráfico da mesma função com pontos diferentes, então, houve observações tanto verbais quanto em registros do tipo “nós formamos o gráfico em forma de U”, mostrando que os alunos reconheceram a curva formada.

Duas duplas não conseguiram obter o gráfico adequado, pois não digitaram em ordem crescente os valores da variável x, mas conseguiram entender o equívoco após a intervenção do professor. Solicitamos que estas duplas discutissem com os outros alunos sobre o formato do gráfico, para que assim pudessem relatar suas observações. Estes não leram o roteiro da tarefa atentamente, mostrando que a utilização exclusiva do roteiro não foi suficiente para o desenvolvimento das tarefas entre estes alunos, ou seja, a mediação do professor se mostrou importante neste processo.

Alguns dos alunos chegaram a comentar que iriam tentar refazer a tarefa em casa, tendo em vista que a maioria tinha um computador com o similar Microsoft Office Excel. Percebemos que eles ficaram interessados em poder utilizar aquele software para conteúdos escolares, porém as duas alunas que tentaram realizar as tarefas afirmaram não terem tido sucesso, alegando que era muito difícil a utilização do software.

Seguindo com a tarefa, retomamos as principais observações obtidas com as atividades anteriores questionando a turma quanto ao formato do gráfico, principalmente se eles acreditavam que a função do segundo grau poderia assumir outra forma gráfica ou se todas seriam assim. Os alunos se mostraram indecisos, com opiniões divididas, assim vemos a importâncias das tarefas proporcionarem várias visualizações e debates para que os alunos, mediados pelo professor, consigam generalizar as hipóteses.

Quando se iniciaria o cálculo do valor da coordenada y do primeiro ponto o projetor deixou de projetar a imagem, assim, para não perder tempo, decidimos continuar a aula explicando os passos no quadro, o que dificultou o entendimento dos alunos, tendo em vista que o oitavo passo exigia mais atenção por conta da abstração.

Consideramos que as construções (quinto passo) se mostraram complexas para os alunos o que fez com que dispersassem, dificultando a comparação com o cálculo manual, ou seja, não relacionando a construção do gráfico com o cálculo da função em um ponto.

Para a conclusão do cálculo do ponto da função, os alunos tiveram que ser auxiliados individualmente, pois era necessário que entendessem como operar no software, e como não tinha apoio do projetor, isso demandou um grande tempo. Neste caso, consideramos que a complexidade do cálculo de um ponto na planilha eletrônica prejudicou o desenvolvimento da tarefa, devido ao tempo gasto para realizá-la.

Após todos conseguirem encontrar o primeiro ponto da função solicitamos que tentassem o mesmo procedimento para o cálculo dos outros dois pontos, desta vez, os alunos demonstraram mais facilidade, pois aprenderam a manusear o software. Acreditamos que a minoria dos alunos relacionou o cálculo por meio da planilha com o cálculo manual.

Por meio de auxílio individual, os alunos obtiveram a tabela requerida e o gráfico da função, neste momento solicitamos que relatassem todas as observações com relação à forma do gráfico da função comparando com o gráfico construído anteriormente. Neste momento, observamos que uma dupla de alunos não havia realizado os cálculos, apenas digitaram na planilha os resultados que os outros alunos tinham obtido e por isso não conseguiam programar a planilha para o cálculo dos outros valores da variável y. Alegaram não “saber fazer a tarefa”, então foi realizada a construção da tabela no computador explicando como a construir.

Depois de disponibilizados alguns minutos para que observassem os gráficos construídos e os comparassem para realizar o relatório, os alunos queriam que o professor contasse e explicasse o que deveria ser observado, diante disso, os indagamos para que eles mesmos observassem situações relevantes ao conteúdo abordado.

Depois das duplas elaborarem seu relatório com as suas observações, com o grande grupo, indagamos os alunos quanto à comparação dos gráficos construídos. A maioria relatou que “um era o contrário do outro”. No registro escrito uma dupla destacou “nós formamos o gráfico em forma de [...] uma montanha, e o passado foi igual o ‘U’[...] é o contrário do primeiro gráfico”.

Quando indagados quanto ao por que os gráficos se apresentavam daquela forma, ou por que eles eram diferentes, não houve manifestações, apesar disso, estes se mostraram intrigados com as questões, então, solicitamos que observassem a função em sua representação algébrica, assim afirmaram que as funções não eram iguais, porém sem relacionar os coeficientes como fatores que modificam o formato da parábola. Então, formalizamos as observações realizadas esclarecendo o efeito do valor do parâmetro “a” no gráfico de uma função do segundo grau.

Apresentação das observações obtidas por meio da aplicação da tarefa proposta

Nessa seção, apresentamos as observações que realizamos durante a aplicação da tarefa subdivididas em três seções: quanto à utilização das tecnologias para o ensino da Matemática; quanto à aprendizagem das funções quadráticas por meio da tarefa; quanto à utilização das tecnologias para a aprendizagem e a visão dos alunos.

Quanto à utilização das tecnologias para o ensino da Matemática

Imprevistos com o funcionamento dos equipamentos podem acontecer e acabar conspirando de forma negativa para a realização das tarefas, portanto é importante o professor testar os equipamentos da escola, ou mesmo solicitar isso a um possível técnico responsável, no caso, não foi possível obter a oportunidade de testar os equipamentos por não ter acesso prévio ao laboratório, por conta da estagiária estar apenas estagiando na escola, entretanto, vale destacar que mesmo testando os equipamentos, o professor sempre deve incluir em seu planejamento um “plano B”, um procedimento ou material extra, para que diante destas situações não coloque em risco o desenvolvimento da aula.

Também é importante destacar que como relatado houve situações em que a dificuldade na utilização do software desfavoreceu a tarefa que não ocorreu como planejado, pois demorou mais do que o previsto, ou seja, observou-se que o tempo é um dos fatores fundamentais para o desenvolvimento de tarefas como as realizadas, pois além da efetivação da construção dos objetos a serem estudados deve haver tempo disponível para a realização das observações e discussões acerca do conteúdo abordado, mediadas pelo professor.

Outro ponto a destacar é que mesmo a maioria dos alunos tendo acesso aos computadores, demonstraram precisar da ajuda do professor para a manipulação do software, o que mostra a importância do educador estar preparado para o uso das tecnologias nas aulas de Matemática. Convém enfatizar que este foi o primeiro contato dos alunos com o software em questão para fins escolares e também a primeira experiência, da então acadêmica, com a regência de uma turma regular.

Tarefas deste perfil apresentam outra possibilidade de visualização dos objetos matemáticos, portanto podem oferecer meios para a realização de tarefas diferenciadas permitindo o desenvolvimento de competências, como discutido nas considerações sobre tecnologias no ensino da Matemática. Além de oportunizar ao aluno o acesso a tecnologias digitais, o que pode despertar o interesse destes.

Acreditamos que se os alunos estivessem familiarizados com o uso de tecnologias digitais no processo de ensino-aprendizagem de Matemática, com a utilização de novas metodologias de ensino e ambientados ao uso do laboratório de informática as tarefas teriam sido realizadas com mais rapidez e teriam sido mais produtivas para a aprendizagem dos alunos, pois, estes não se dispersariam em construções de objetos matemáticos e não se mostrariam tão dependentes do professor para a realização de observações importantes que devem ser feitas pelos alunos para a confirmação da aprendizagem. Entretanto, é necessário um primeiro passo, então o professor precisa começar a trabalhar com tecnologias digitais para que os alunos possam ambientar-se e com o tempo, tanto professor quanto aluno, podem aproveitar muito mais as potencialidades das tecnologias digitais tanto no ensino quanto na aprendizagem.

Neste sentido, quanto à utilização das tecnologias no ensino da Matemática, estas se constituem importantes ferramentas de ensino e aprendizagem, porém, necessitam planejamento prévio.

Quanto à aprendizagem das funções quadráticas por meio da tarefa em questão

Ao refletir sobre os resultados da tarefa verificamos que, de maneira geral, atingimos o objetivo inicial, embora existam situações que após reflexões sobre o desenvolvimento, consideremos que em outra aplicação seriam aperfeiçoadas. Tendo em vista a experiência adquirida com a aplicação desta tarefa, consideramos que é necessária a compreensão do cálculo de um ponto da função antes de propor a construção do gráfico na planilha eletrônica, portanto, é necessário esclarecer isto com os alunos, também verificamos a necessidade de incluir no roteiro observações e tarefas de comparações entre o cálculo manual e o cálculo na planilha eletrônica antes de iniciar a inserção dos pontos da função, para que assim não se acumulem tantas informações em apenas um passo do roteiro.

Outro fato é a relação entre os pontos que formam a função, que deveria ser mais explorada, com incentivos para que os alunos plotassem mais pontos, construíssem gráficos diferentes, utilizando valores positivos e negativos para o x, e questionando o que isso alteraria no gráfico. Nesta oportunidade pelo nervosismo do estágio supervisionado, inexperiência e a falta de tempo para mais observações, uma vez que, para estas dispusemos apenas dos quinze minutos finais, não foram realizadas estas discussões.

Por outro lado, pela decepção daqueles que não conseguiram inserir o gráfico adequadamente por equívocos na construção, percebemos que queriam descobrir o formato do gráfico, por si mesmos, ou seja, observar a forma do gráfico daqueles pontos por meio do seu gráfico (do próprio aluno), pois queriam refazer a construção, mas não houve tempo suficiente. Destacamos então a importância de possibilitar aos alunos a construção da representação do objeto matemático para seu estudo, pois isso contribui para que adquiram e desenvolvam o conhecimento, viabilizando situações em que se tornam ativos em seu processo de aprendizagem da Matemática. Nesse sentido, consideramos que nossa experiência foi de suma importância para o aperfeiçoamento da tarefa e também para a aquisição de experiência.

Quanto à utilização das tecnologias para a aprendizagem dos alunos

 Observamos com a atitude destes alunos, que para que ocorra a aprendizagem é necessário conseguir a atenção e interesse deles para o sucesso das tarefas o que nem sempre é algo simples, pois cada indivíduo possui interesse particular. No início da realização da tarefa, quando os alunos precisaram explorar as construções, observamos seu estranhamento, insatisfeitos com os rumos da atividade. Porém após intervenções do professor por meio de questionamentos, a maioria dos alunos se engajou, embora, apresentassem muito receio de explicitar suas observações por medo de errar.

 Essa insegurança pode ser reflexo de aulas, exclusivamente baseadas em metodologias “tradicionais”. Percebemos que sem o aval do professor os alunos não acreditavam em suas observações, mesmo visualizando via interface do software e narrando conjecturas não as registraram no relatório, por apresentarem dificuldade na transcrição ou como se ainda não se sentissem convencidos.

Acreditamos que os alunos não são acostumados com tarefas em que precisem de leitura, interpretação, raciocínio e capacidade de pensamento criativo para explicar situações como a apresentada na tarefa, pois, quando colocados em situações que exigiam estas habilidades para o seu desenvolvimento, apresentaram muita dificuldade.

Por outro lado, a realização das tarefas proporcionou observações que seriam muito difíceis de serem feitas apenas com a utilização do quadro e giz ou papel e caneta. Houveram observações interessantes, além das esperadas, como: “o maior número negativo é o -1”. Embora, esse seja um conceito que os alunos já deviam ter conhecimento, a observação do aluno, mostra que foi durante o desenvolvimento da tarefa que compreendeu a ordem nos inteiros. Neste caso, observam-se as possibilidades que as tecnologias oferecem.

Também com relação a esta tarefa, observamos que eles não copiavam as conclusões um do outro, queriam descobri-las sozinhos, ou pelo menos visualizá-las e relacioná-las ao seu objeto matemático, portanto as tecnologias juntamente com metodologias de ensino adequadas possibilitam o aluno desenvolver habilidades como observação, criatividade, pensamento matemático e sua capacidade de relatar e argumentar sobre o objeto matemático observado. Entretanto, como alerta Mercado (2012), é importante reconhecer que o uso das tecnologias não resolve todos os problemas e desafios propostos pelo ensino e aprendizagem, mas podem se apresentar ferramentas úteis para contribuir no processo de ensino e aprendizagem.

Uma vez que as tecnologias digitais ainda não integram a prática docente de muitos professores nas escolas públicas brasileiras, seu uso causa estranhamento para alunos que acham que tarefas que as utilizem são lúdicas, e não ajudam na aprendizagem, que o professor não está ministrando a aula corretamente, como verificamos em respostas obtidas através do questionário respondido pelos alunos referentes às tarefas realizadas no laboratório de informática. Tais respostas revelam que esses alunos não experenciaram tarefas com uso de computadores que possibilitassem o desenvolvimento da capacidade de observar fatos matemáticos, questioná-los, conjecturar sobre eles, e apenas os aprenderam de forma expositiva e mecânica. Portanto, observamos a necessidade do professor propor tarefas que possibilitem desenvolver as habilidades citadas, afinal é o professor o responsável pelo planejamento e execução das tarefas a serem realizadas durante as aulas.

Considerações Finais

Apesar dos imprevistos, principalmente com problemas técnicos, o uso das tecnologias digitais é muito gratificante, pois possibilita que o aluno reflita e visualize elementos matemáticos. O dinamismo proporcionado pelos softwares aguça a curiosidade e permite conjecturas a respeito aos conteúdos matemáticos envolvidos, o que favorece debates e a formulação de argumentos. Com isso, os alunos constroem seus conhecimentos, e não apenas os recebem do professor de forma passiva.

Nesta oportunidade em que realizamos as tarefas os estudantes não tinham contato com alternativas diferenciadas de ensino, apesar de já utilizarem o laboratório de informática algumas vezes, porém não para iniciar um conteúdo, e não com o BrOffice Calc. Assim é natural que ocorra estranhamento por parte dos alunos, já que passaram praticamente toda a vida escolar tendo apenas aulas expositivas. Como ressalta Gravina e Santarosa (1998, p. 21) “pode-se dizer que os ambientes informatizados apresentam-se ainda como simples ferramentas de suporte ao processo de ensino e aprendizagem. Está-se procurando mudança nos métodos, a partir da incorporação dos novos recursos”.

É fato que alguns alunos não se sentiram a vontade para realizar tarefas nas quais precisem resolver questões que não seguem um modelo, e assim permaneciam a espera do auxílio do professor, o que pode ter ocorrido por não confiarem em suas conjecturas ou pode ser reflexo da forma letárgica que sempre receberam os conteúdos.

Entretanto, 89% dos estudantes alegaram preferir aulas no laboratório de informática e avaliaram as atividades boas, segundo o aluno A por aprender de um “jeito diferente”, “dinâmico e mais fácil de entender a matéria” segundo o aluno B, foi bom, pois “aprendi a mexer em um programa que não sou muito chegado”. Conforme o aluno A “fica muito mais fácil fazer os gráficos do que [...] fazer na mão”. Além disso, 95% revelam que gostaram das atividades desenvolvidas no laboratório de informática.

Reiteremos que há muitas questões envolvidas no que diz respeito à integração das tecnologias na prática docente, como preparo dos professores e disponibilização de espaço e equipamentos de qualidade, porém são evidentes os resultados positivos obtidos com a utilização dos recursos tecnológicos no ensino e aprendizagem da Matemática, como observado, assim, acreditamos ser imperativa a realização de investimentos para a quebra de paradigmas nas escolas brasileiras, além de incentivos à profissão do professor para que cada vez mais busque renovar e aperfeiçoar sua prática. Deste modo, com a inserção das tecnologias digitais almejamos que a qualidade do ensino da Matemática possa melhorar, possibilitando aulas mais dinâmicas, nas quais os alunos possam exercer papel ativo frente à aprendizagem da Matemática.