Introdução

Na matemática moderna, o plano euclidiano pode ser definido axiomaticamente através de um conjunto de axiomas a que devem satisfazer os pontos e as retas considerados como objetos primitivos e, a partir dos quais, se podem estabelecer rigorosamente todos os resultados da geometria euclidiana plana. Existem vários sistemas axiomáticos modernos (e. g., o sistema de Hilbert, o sistema de Birkhoff) que foram desenvolvidos de modo a dar uma apresentação completamente rigorosa (do ponto de vista da matemática moderna) da abordagem da geometria proposta por Euclides nos seus Elementos. Esta abordagem baseia-se, para além das noções comuns, nos cinco seguintes axiomas que enunciamos seguindo Barbosa (2009, p. 2):

Axioma 1: Pode-se traçar uma (única) reta ligando quaisquer dois pontos.

Axioma 2: Pode-se continuar (de uma única maneira) qualquer reta finita continuamente em uma reta.

Axioma 3: Pode-se traçar um círculo com qualquer centro e com qualquer raio.

Axioma 4: Todos os ângulos retos são iguais.

Axioma 5: É verdade que, se uma reta ao cortar duas outras, forma ângulos internos, no mesmo lado, cuja soma é menor do que dois ângulos retos, então as duas retas, se continuadas, encontrar-se-ão no lado onde estão os ângulos cuja soma é menor do que dois ângulos retos.

Chamando paralelas a duas retas (do plano) que não se intersetam, o quinto axioma é muitas vezes, nas axiomáticas modernas, substituído pelo famoso

Axioma das Paralelas: Por um ponto exterior a uma reta pode-se traçar uma única reta paralela à reta dada.

Aquele enunciado, também chamado às vezes de Axioma de Playfair, faz parte dos possíveis substitutos para o quinto postulado de Euclides que foram produzidos durante a longa procura de uma demonstração a partir dos quatro primeiros axiomas (Barbosa, 2009). Esta procura concluiu-se finalmente no século XIX pela emergência da geometria hiperbólica. Axiomaticamente, a geometria hiperbólica plana, cujos fundadores são C. F. Gauss (1777-1855), N. Lobachevsky (1792-1856) e J. Bolyai (1802-1860) (Barbosa, 2009), é definida por todos os axiomas do plano euclidiano a menos do axioma das paralelas que é substituído pelo:

Axioma hiperbólico: Por um ponto exterior a uma reta pode-se traçar pelo menos duas retas paralelas à reta dada.

O conjunto R² constitui um modelo do plano euclidiano no sentido em que os pontos, definidos como sendo os elementos de R², e as retas, definidas pelas equações usuais, verificam todos os axiomas do plano euclidiano. Da mesma forma, um modelo do plano hiperbólico é dado por uma noção concreta de pontos e retas que satisfazem todos os axiomas do plano hiperbólico. Os primeiros modelos do plano hiperbólico foram desenvolvidos por E. Beltrami (1835-1900), H. Poincaré (1854-1912) e F. Klein (1849-1925) (Stillwell, 1996).

Na primeira secção deste texto vamos apresentar o modelo chamado de Disco de Poincaré bem como alguns aspetos fundamentais da geometria hiperbólica plana e, na segunda secção, apresentaremos uma construção de uma pavimentação do Disco de Poincaré por polígonos regulares.

Disco de Poincaré

Este modelo define-se em ambiente euclidiano em que vai ser introduzida uma noção de pontos e de retas hiperbólicas. Mais precisamente considera-se, no plano euclidiano, um disco limitado por uma circunferência unitária que vamos designar por circunferência limite e chamamos (ver Figura 1):

• pontos hiperbólicos aos pontos interiores ao disco;

• retas hiperbólicas aos diâmetros do disco e aos arcos de circunferência ortogonais à circunferência limite.

Figura 1. Retas Hiperbólicas

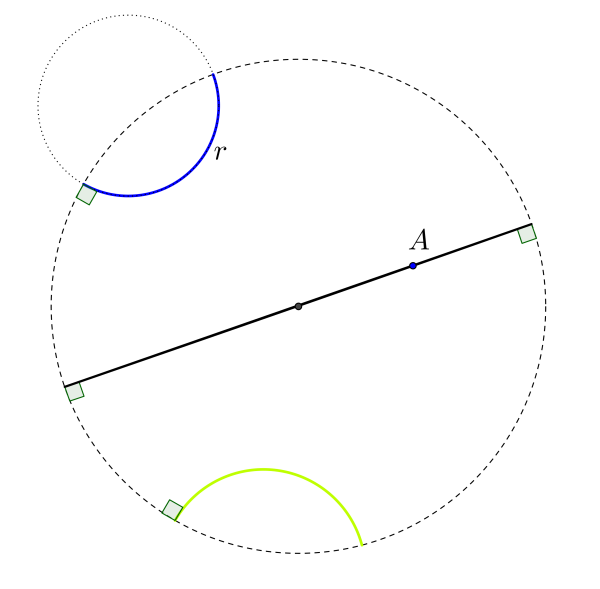
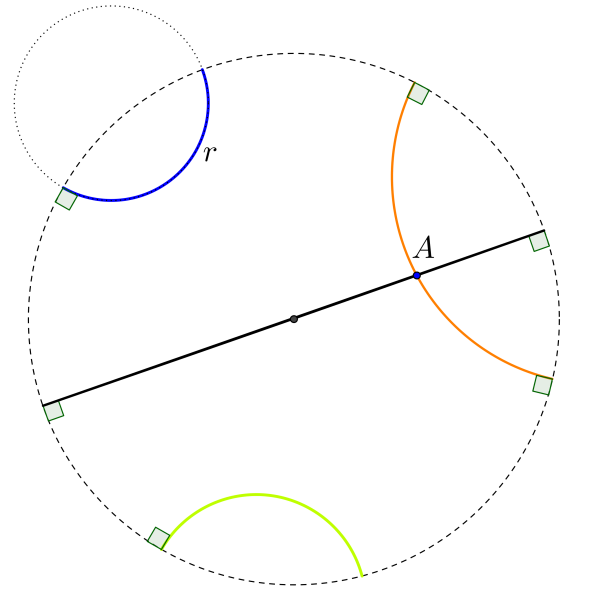
Continuando a chamar paralelas às retas que não se intersetam podemos verificar que, no Disco de Poincaré, o Axioma das Paralelas não se verifica mas sim o Axioma Hiperbólico pois, pelo ponto A, exterior a r, passam duas retas hiperbólicas paralelas a r (ver Figura 2).

Todos os outros axiomas do plano euclidiano se verificam. Exemplificamos aqui, com auxílio do Geogebra, a construção de uma reta hiperbólica. Esta construção, tal como muitas outras no plano hiperbólico, usa de forma fundamental a inversão circular, já disponível no Geogebra, e as suas propriedades.

Figura 2. Retas hiperbólicas paralelas

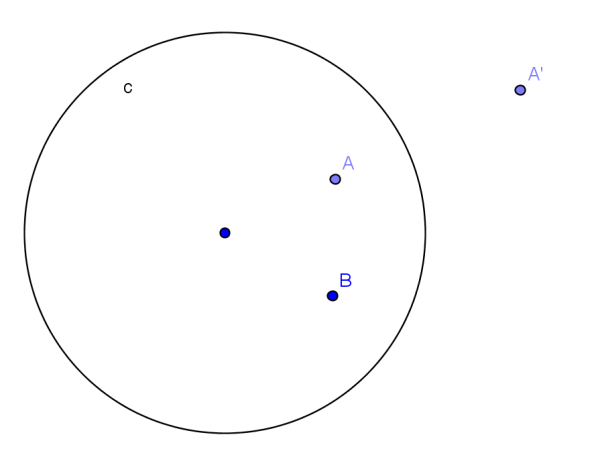
Recorde-se que, considerando uma circunferência C de centro O e raio r e A um ponto distinto de O, o inverso de A relativamente a C é o ponto A’ pertencente à semirreta ÒA (ver Figura 3) que verifica a condição:

             Figura 3. Inversão na Circunferência  

Na perspetiva de construir no Geogebra a única reta hiperbólica que passa por dois pontos distintos A e B, vamos utilizar a seguinte propriedade da inversão:

Uma circunferência C’ que passa por um ponto é ortogonal a C se e somente se C’ contém o inverso desse ponto em relação a C.

Supondo, em primeiro lugar, que os pontos A, B e O não estão alinhados procederemos à sequência dos seguintes passos no Geogebra:

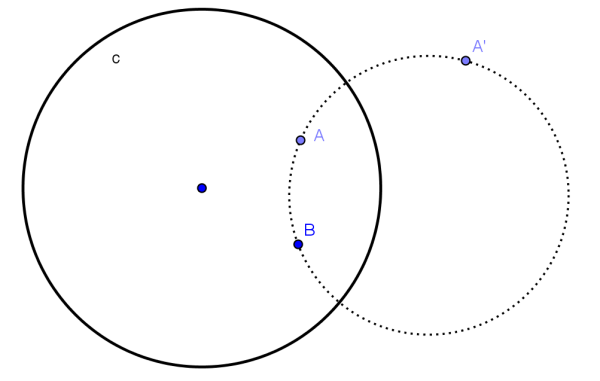
• marcar os pontos A e B e construir o inverso A’ de A em relação à circunferência limite (ver Figura 4);

Figura 4. A’ ponto inverso de A

• construir, usando o comando Circunferência (Três Pontos) a circunferência d que contém os pontos A, B e A’ (ver Figura 5). Note-se que esta circunferência é ortogonal à circunferência limite;

Figura 5. Circunferência d

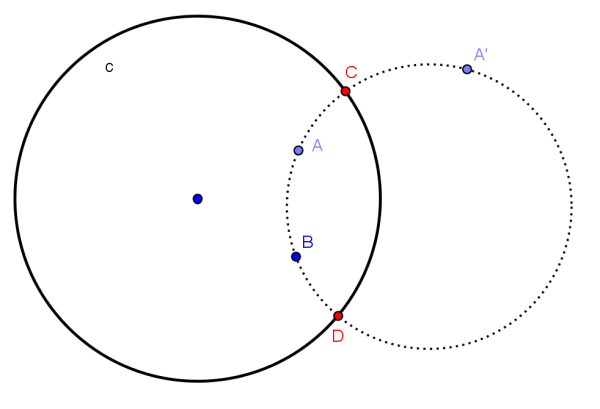
• marcar os pontos de interseção de d com a circunferência limite que designamos por C e D (ver Figura 6);

Figura 6. Pontos C e D

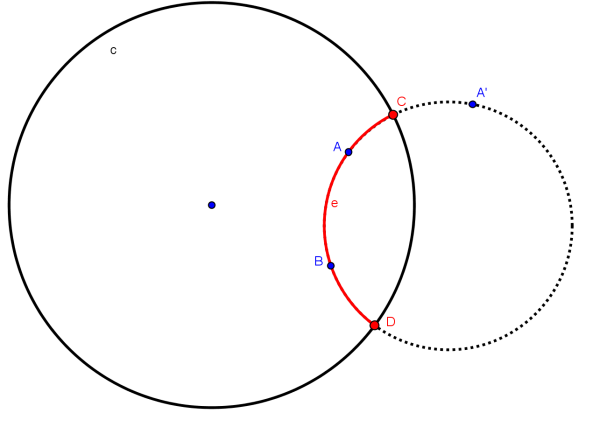
• definir, usando o comando Arco Circuncircular (Três Pontos), selecionando os pontos C, A e D, nesta ordem, o arco de circunferência que contém os pontos e C e D o ponto A (ver Figura 7). Este arco é a reta hiperbólica e que contém A e B.

Figura 7. Reta Hiperbólica

Usando as ferramentas indicadas, os passos anteriores permitem de facto construir a reta hiperbólica no caso de A e B estarem alinhados com o ponto O tendo contudo atenção que o ponto A seja diferente do ponto O. Nesta caso a construção produzirá o diâmetro que passa por A.

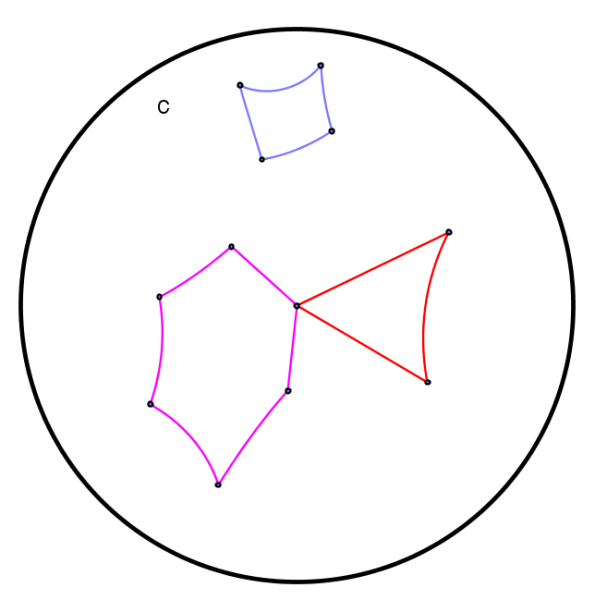
Assim, neste ponto, podemos proceder à criação de uma ferramenta própria do Geogebra que nos levará à criação imediata de uma reta hiperbólica. Para tal basta definir como objetos iniciais os pontos A e B e a circunferência limite e, como objetos finais, o arco de circunferência e. Tal ferramenta bem como outras para construções básicas no Disco de Poincaré (Semirretas, segmentos de reta, triângulos, polígonos, etc… (ver Figuras 8 e 9)) foram construídas no âmbito da tese de mestrado intitulada O plano hiperbólico (Maia, 2011).

Figura 8. Semirreta e segmento de reta hiperbólicos

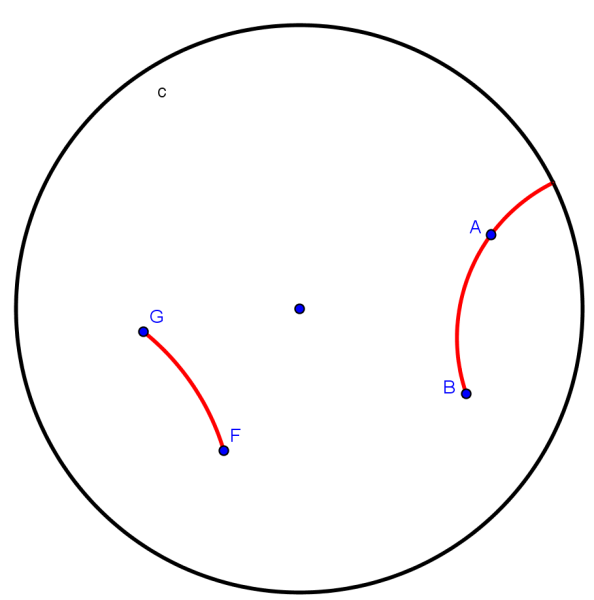
Figura 9. Polígonos hiperbólicos

No GeogebraTube existem pacotes disponíveis para fazer construções no Disco de Poincaré através da utilização da ferramenta respetiva tais como o que está acessível em http://www.geogebratube.org/material/show/id/14079.

Finalmente salientam-se alguns aspetos importantes do Disco de Poincaré bem como alguns resultados fundamentais sobre os triângulos hiperbólicos:

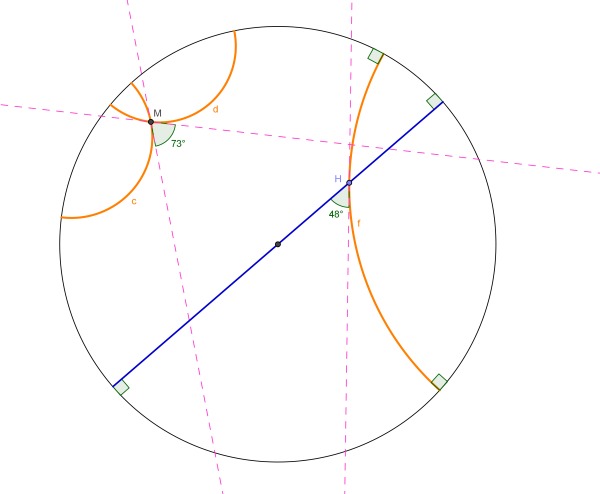
• no Disco de Poincaré, a medida do ângulo entre duas semirretas é dada pela medida, no plano euclidiano,  entre as semirretas tangentes às semirretas consideradas, no ponto de interseção (ver Figura 10).

Figura 10. Ângulos hiperbólicos

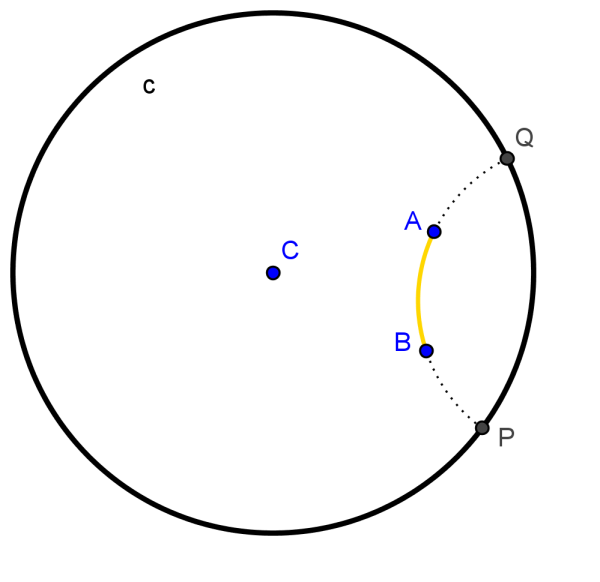
• no Disco de Poincaré, a distância (hiperbólica) entre dois pontos A e B (ver Figura 11) é dada por:

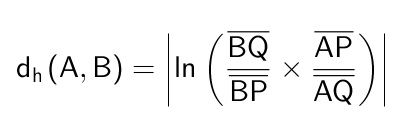
• onde P e Q são os pontos “limites” da reta hiperbólica AB.

Figura 11. Distância hiperbólica

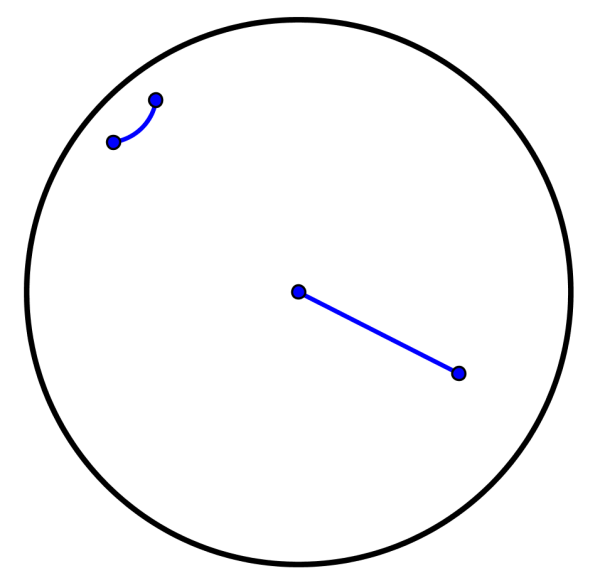
Repare-se que os dois segmentos de reta da figura 12 têm, segundo um olho euclidiano, comprimentos distintos mas são congruentes relativamente à distância hiperbólica.

Figura 12. Segmentos hiperbólicos congruentes

• Num triângulo hiperbólico, a soma dos ângulos internos é sempre menor do que 180º.

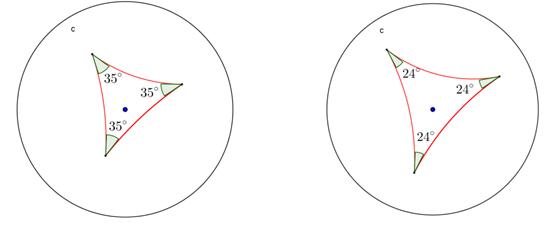
Também se salienta que, no plano hiperbólico, não existem triângulos semelhantes que não sejam congruentes, por exemplo, os dois seguintes triângulos equiláteros não são semelhantes (ver Figura 13).

Figura 13. Triângulos hiperbólicos equiláteros

As Pavimentações no Disco de Poincaré usando o Geogebra

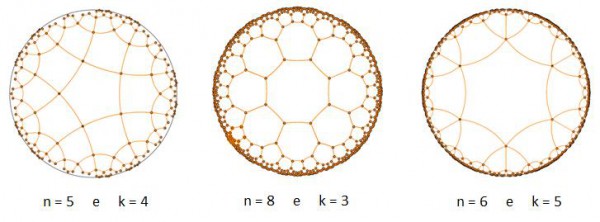
Como sabemos, na Geometria Euclidiana, há apenas três polígonos que pavimentam de forma regular o plano: o triângulo equilátero, o quadrado e o hexágono regular. Na Geometria Hiperbólica, há infinitas formas de pavimentar o Disco de Poincaré que dependem de dois parâmetros: do número de lados do polígono regular (n) e do número de polígonos regulares que concorrem em cada um dos vértices (k). Vejamos alguns exemplos destas pavimentações na Figuras 14.

Figura 14. Pavimentações do Disco de Poincaré

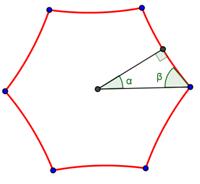
Considerando no polígono regular inicial o triângulo retângulo tal como indicado na Figura 15, podemos verificar que

Por outro lado, para que concorram k polígonos em cada vértice é necessário que

Por se se tratar de triângulo hiperbólico temos necessariamente que

ou seja

Figura 15. Triângulo Retângulo Fundamental

Por um Teorema de Poincaré sabemos de facto que esta condição também é suficiente para a existência da pavimentação na base deste polígono regular com n lados (ver por exemplo Iversen, 1992). Contudo, para construir a pavimentação do Disco de Poincaré há certos cuidados que precisamos de ter para além de cumprir esta condição. Por exemplo, se tomarmos n=6 e k=4 e iniciarmos a pavimentação começando por representar um hexágono regular (ver Figura 16) e se continuarmos, tal como na Geometria Euclidiana, a fazer reflexão (neste caso inversão circular) do polígono em relação a cada um dos lados obter-se-ia a segunda camada de hexágonos (ver Figura 17):

Figura 16. Hexágono regular

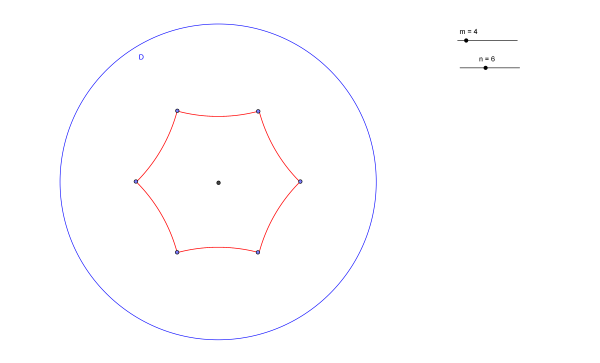
 Figura 17. Inversão circular do primeiro hexágono

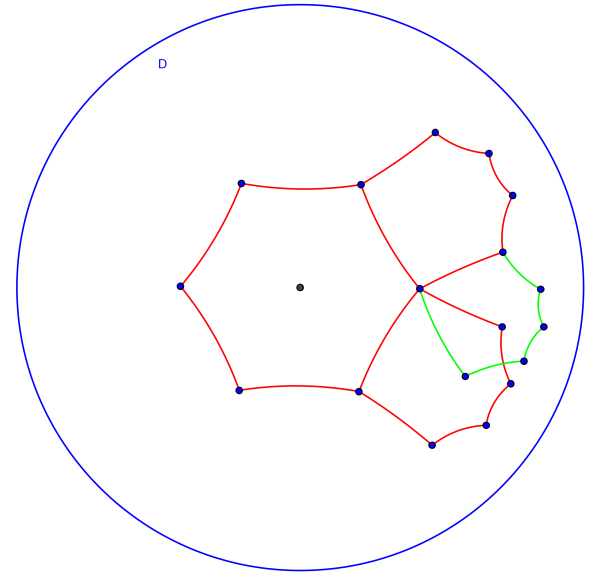
A partir desta segunda camada de hexágonos repetiríamos novamente o processo e o hexágono a verde (ver Figura 18) ficaria sobreposto o que não permitiria produzir uma pavimentação.

Figura 18. Sobreposição Indesejável

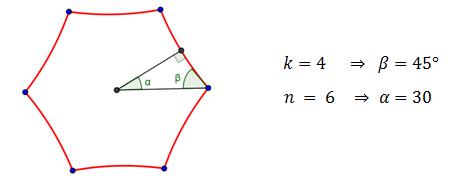
Analisando cuidadosamente esta construção, os ângulos internos do triângulo representado no interior do hexágono têm de amplitude 90º, 30º e 48º (ver Figura 19) mas, para que concorram quatro hexágonos regulares em cada um dos vértices, os ângulos internos do triângulo teriam de ter, de medida de amplitude 90º, 30º e 45º (ver Figura 20).

Figura 19. Ângulos internos verificados

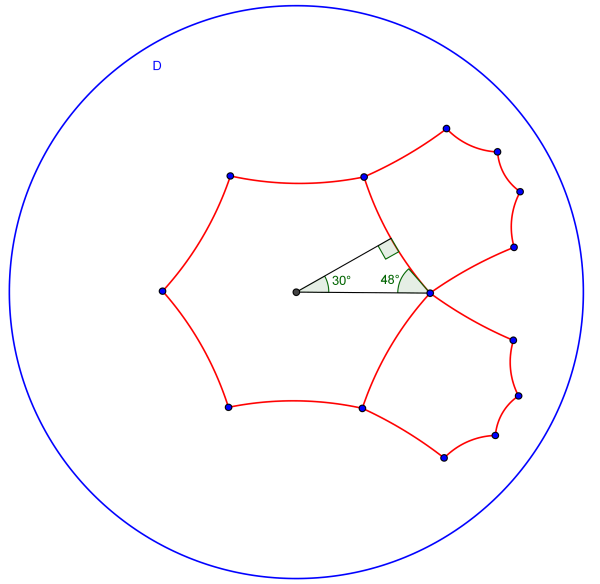
Figura 20. Ângulos internos pretendidos

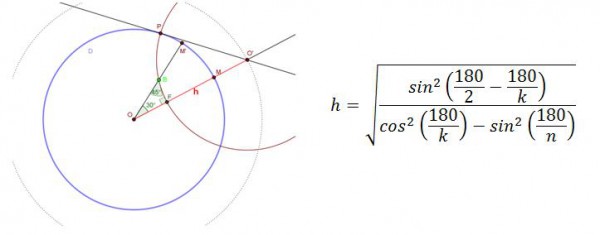
O que permite controlar o ângulo β é a seguinte relação entre os inteiros n e k e o comprimento h do segmento  onde O’ é o centro da circunferência suporte do lado oposto ao ângulo α (Coxeter, 2003; Maia, 2011) (ver Figura 21).

Clique na Figura 21 para experimentar um applet com a construção do triângulo fundamental dependente do valor atribuído a n e a k que podem ser modificados a partir do seu seletor.

Figura 21. Triângulo inicial

A partir daqui, fazendo reflexões sucessivas dos lados do triângulo [OFB] obteríamos o hexágono representado na Figura 16. Continuando as inversões circulares conseguiríamos pavimentar todo o Disco de Poincaré. Na base deste processo é possível construir uma ferramenta, no Geogebra, que permita pavimentar regularmente o Disco de Poincaré tendo como dados iniciais os valores dos parâmetros n e k previamente definidos.

Um processo análogo ao que foi descrito foi utilizado e disponibilizado por Piman em

http://www.geogebra.org/en/upload/files/piman/PoincareDisk/H_regular_tesselations.html