Introdução

A visão construtivista do ensino, aliada aos propósitos da aprendizagem da matemática escolar, realça a importância do desenvolvimento da criatividade matemática do estudante (Lev-Zamir & Leikin, 2011) e enfatiza o valor crescente que é atribuído à utilização de ambientes de geometria dinâmica (AGD) na sala de aula.

Ao longo dos últimos anos, na matemática escolar, os teoremas e as demonstrações em Geometria têm sido apresentadas aos estudantes quase sempre como um produto acabado sem que estes tenham o prazer das suas descobertas, das suas explorações e investigações (King & Schattschneider, 1997). Para o desenvolvimento destas tarefas, tal como é referido no Programa de Matemática de 2007 (ME, 2007), o recurso a software de geometria dinâmica permite o desenvolvimento da intuição geométrica, da capacidade de visualização e o estabelecimento de “uma relação mais afectiva com a Matemática” (p. 51). Os AGD constituem um meio poderoso para testarem conjeturas e encontrarem contraexemplos (Villiers, 2003) através do desenho concreto e, no geral, permitir “aos alunos fazer descobertas de forma autónoma” (Keyton, 2003, p. 79). Nesta perspetiva e pelo facto de as atividades de exploração com recurso a estes programas serem praticamente inexistentes no percurso escolar dos nossos estudantes (Licenciatura em Educação Básica), como serão as suas reações face à investigação autónoma? Serão capazes de produzir evidências matemáticas em relação ao objeto apresentado?

Enquadramento Teórico

Os ambientes de geometria dinâmica facilitam a visualização, a exploração e a transformação de imagens que, em Geometria, ajudam a desbravar caminhos, a iluminar uma solução ou mesmo a detetar caminhos erróneos. Esta Geometria que é própria para o ensino básico afasta-se das manipulações algébricas para a resolução de problemas geométricos que, nos últimos anos, tem conquistado terreno a esta área da matemática. No ensino, este facto, para além de não aumentar a capacidade de visualização, originou praticamente o desaparecimento de aspetos ligados à observação, experimentação e construção de objetos geométricos (Abrantes, Serrazina & Oliveira, 1999). Já Lacroix (1765-1843) dizia que, pelo facto da manipulação algébrica não garantir a compreensão geométrica do que se está a executar, a álgebra e a Geometria deviam ser tratadas separadamente (Boyer, 1998). Para além desta problemática, na sala de aula há um apelo sistemático à capacidade de abstração por parte dos alunos que nem sempre está acessível a todos. Almeida (1994) escreve que “imaginar exige de quem o faz, não ver tudo o que se vê e ver algo do que não se vê” (p. 7). No mesmo sentido Pimenta (2007), referindo-se especificamente às isometrias mas cuja problemática é visível noutras temáticas da Geometria, apresenta o seguinte exemplo:

Em muitas aulas sobre isometrias vive-se num mundo imaginário:  - “imaginem este triângulo a rodar 180 graus em torno deste vértice”; – “imaginem que se move a figura, sem lhe alterar o tamanho, do canto do quadro até ao centro do quadro” (p. 37).

Segundo Ferreira e Vale (2013) explorar, justificar e conjeturar são processos que existem nas várias áreas da Matemática e em todos os ciclos de ensino. Para as autoras é através do raciocínio que os estudantes aprendem matemática e “dão significado às ideias matemáticas (geométricas em particular) bem como aos procedimentos que executam” (p. 82). De acordo com Pimentel e Vale (2012) é habitual considerarem-se dois tipos fundamentais de raciocínio: indutivo e dedutivo. O indutivo parte do particular para o geral, da observação de dados sobre os quais se formulam hipóteses exploratórias, e, com base noutros casos, se generaliza para um conjunto mais amplo. O dedutivo nasce da necessidade de se verificar a autenticidade dessa generalização, baseando-se em argumentos lógicos do tipo modus ponens. Davis e Hersch (1995) afirmam que toda a matemática se consubstancia nesta necessidade de prova.

Alguns autores (e.g., Radford, 2008), com base no trabalho de Peirce, identificam outro tipo de raciocínio: o raciocínio abdutivo. De acordo com a Stanford Encyclopedia of Philosophy (2010), Peirce apresenta a abdução como uma fase criativa, de produção de hipóteses a explorar, tornando-se assim óbvio como as ideias aparecem na nossa mente. Nesta fase pode prognosticar-se uma conclusão de forma incompleta, ainda sem dedução, mas não será possível validar dedutivamente um resultado sem uma conjetura prévia. Enquanto a abdução consiste em escolher uma hipótese, a indução envolve a sua testagem (Rivera & Becker, 2007). A abdução é o processo de introdução de novas ideias, a formulação de explicações ou conjeturas das quais alguma pode ser testada no processo de indução; a indução corresponde ao passo seguinte, o teste da conjetura em mais dados. Para estes autores, o processo de generalização acontece quando há aceitação de uma forma geral obtida por um processo cíclico de abdução e indução. No fim deste ciclo surge a dedução, que envolve explicação, argumentação e prova.

As três fases do raciocínio estão também refletidas na definição de Lannin, Ellis e Elliot (2011): “o raciocínio matemático é um processo evolutivo que inclui conjeturar, generalizar, investigar porquê, e desenvolver e avaliar argumentos” (p. 10). Estes autores estabelecem um tipo de raciocínio matemático que relaciona de forma interativa a conjetura e generalização, a justificação ou refutação e a compreensão do porquê.

As ideias principais destes três tipos de raciocínio podem ser sintetizadas do seguinte modo: a abdução cria, a indução verifica e a dedução explica.

A utilização de programas de geometria dinâmica veio alterar profundamente a forma de ensinar e a possibilidade de serem os estudantes a criar matemática nova e, consequentemente torná-los “mais envolvidos na sua própria aprendizagem” (Garry, 2003, p. 69). Já o programa de matemática de 2007 recomendava que:

os alunos devem recorrer a software de Geometria Dinâmica, sobretudo na realização de tarefas exploratórias e de investigação. (…) Tanto os recursos computacionais, como os modelos geométricos concretos permitem desenvolver a intuição geométrica, a capacidade de visualização e uma relação mais afectiva com a Matemática (Ministério da Educação, 2007, p. 51).

O apoio fornecido pelos AGD na solução de problemas abertos que exigem a formulação de uma conjetura atesta o seu potencial didático (e.g., Arzarello, Olivero, Paola & Robutti, 2002; Boero, Garuti & Lemut, 2007; Hadas, Hershkowitz & Schwarz, 2000; Olivero 2001). Segundo Harel e Sowder (1998, citado por Balacheff, 2008) uma conjetura é:

uma observação feita por um sujeito que não tem qualquer dúvida sobre a sua veracidade. A observação faz com que deixe de ser uma conjetura e torna-se um facto a partir do momento em que o sujeito esteja certo da sua veracidade (p. 504).

Do ponto de vista educacional, Itzcovich (2007, p. 17) argumenta que a ideia de conjeturas “é a produção de uma ‘suspeita’, um ‘olhar’, produto da experiência de trabalho” (p. 17). Para este autor a exploração de conjeturas “reúne tentativa e erro, utilizando-se os dados conhecidos e conhecimentos disponíveis que permitem uma informação com um certo grau de certeza” (p. 17).

Muitos investigadores realçam a importância do levantamento de conjeturas como uma atividade prévia à demonstração (e.g., Mariotti, 2012; Pedemonte, 2008). Durante a produção de uma conjetura, o estudante desenvolve progressivamente a sua declaração através de uma intensa atividade argumentativa. Mais tarde, no processo de provar essa afirmação, o estudante liga coerentemente algumas das justificações (argumentos) produzidas na construção da afirmação. Para Mariotti (2012) as tarefas de investigação que exigem “provar …” se uma certa afirmação é verdadeira não são eficazes para desencadear a produção de argumentos. As propostas mais eficazes estão relacionadas com as atividades que requerem a produção de uma conjetura (Mariotti, 2012; Pedemonte, 2008). Embora não se deva avaliar a dificuldade que os alunos enfrentam em perceber e interpretar os fenómenos dinâmicos que ocorrem no ecrã (e.g., Talmon & Yerushalmy 2004; Baccaglini-Frank, Mariotti & Antonini, 2009), o potencial oferecido por um AGD no suporte aos processos de conjeturas dá um profundo valor educacional às atividades de conjeturas propostas por problemas abertos e motiva o esforço solicitado na promoção do mesmo, através de intervenções pedagógicas adequadas.

O Geogebra é um programa de geometria dinâmica, com um interface intuitivo e livre de custos, que tem sido fortemente divulgado e reconhecido pela comunidade matemática nacional e internacional. Com o Geogebra a Geometria torna-se mais ativa, mais rigorosa sob o ponto de vista das construções e com maiores potencialidades no campo da investigação uma vez que é possível, de uma forma rápida, fazer múltiplas tentativas na procura da solução, experimentar e encontrar conjeturas, desenvolver a capacidade de visualização, transformar e simular (King & Schattschneider, 1997). A investigação mostra que, quando os professores de matemática aprendem a trabalhar com o Geogebra e se apercebem das suas capacidades e potencialidade, ficam ansiosos por incorporar o programa nas suas próprias salas de aula. Felizmente, com a proliferação de quadros interativos e projetores, o Geogebra tem uma saída pronta para explorar, de forma dinâmica, a matemática numa grande tela.

Muitas vezes os estudantes atribuem a dificuldade em Geometria aos vários anos de ensino da matemática onde se pressupunha a memorização de teoremas e de provas escritas (Senk, 1989). Há certamente mais Geometria para além das provas e teoremas, no entanto, a responsabilidade de mudar tais atitudes nos estudantes encontra-se no professor em sala de aula. Seguindo a recomendação de Fuys (1985) um bom começo será o de dar aos estudantes experiências de níveis mais baixos antes de se lhes pedir para fazerem provas formais.

Contexto metodológico

Na sequência das linhas de pensamento de Senk (1989) e Fuys (1985) e crentes nos benefícios do uso de ambientes dinâmicos quer pelos contributos apontados pela comunidade matemática quer pelo reconhecimento por parte dos estudantes em anos anteriores, decidimos propor aos estudantes de Educação Básica, futuros professores, uma tarefa que lhes permitisse criar matemática, ou seja, potenciar a possibilidade de experimentar, conjeturar, descobrir teoremas e demonstrar. Esta experiência de ensino teve como foco a exploração de polígonos que não eram conhecidos pelos estudantes – os polígonos médios de polígonos definidos inicialmente – utilizando para tal o Geogebra.

Os estudantes que participaram nesta tarefa pertenciam ao 3.º ano da Licenciatura em Educação Básica (LEB) e frequentavam uma Unidade Curricular (UC) de opção denominada Matemática, Materiais e Tecnologias. Esta UC prevê a exploração de um programa de geometria dinâmica, o Geogebra, para o ensino e aprendizagem da matemática no Ensino Básico. No ano letivo anterior, estes estudantes já tinham frequentado, alguns sem sucesso, uma UC de Geometria cujo programa inclui a construção de diversos objetos geométricos através de materiais de desenho. Este grupo de estudantes possuía backgrounds na área da matemática claramente distintos: uns estudaram matemática A, B ou MACS no ensino secundário, outros, disciplinas de matemática do ensino profissional, outros já não tinham matemática desde o 9.º ano de escolaridade.

A tarefa de investigação proposta decorreu, no ano letivo de 2013/14, numa aula com a duração de duas horas e teve como objetivos: (a) propor a pares de estudantes a descoberta de conjeturas relacionadas com o novo polígono (polígono médio); (b) a verificação da sua veracidade em casos particulares e posterior dedução geométrica ou, pelo contrário, a procura de contraexemplos para a refutação da mesma, seguindo o esquema representado na Figura 1 adaptado de um outro proposto por Villiers (2003, p. 31).

 Figura 1. As Várias Fases da Tarefa de Investigação

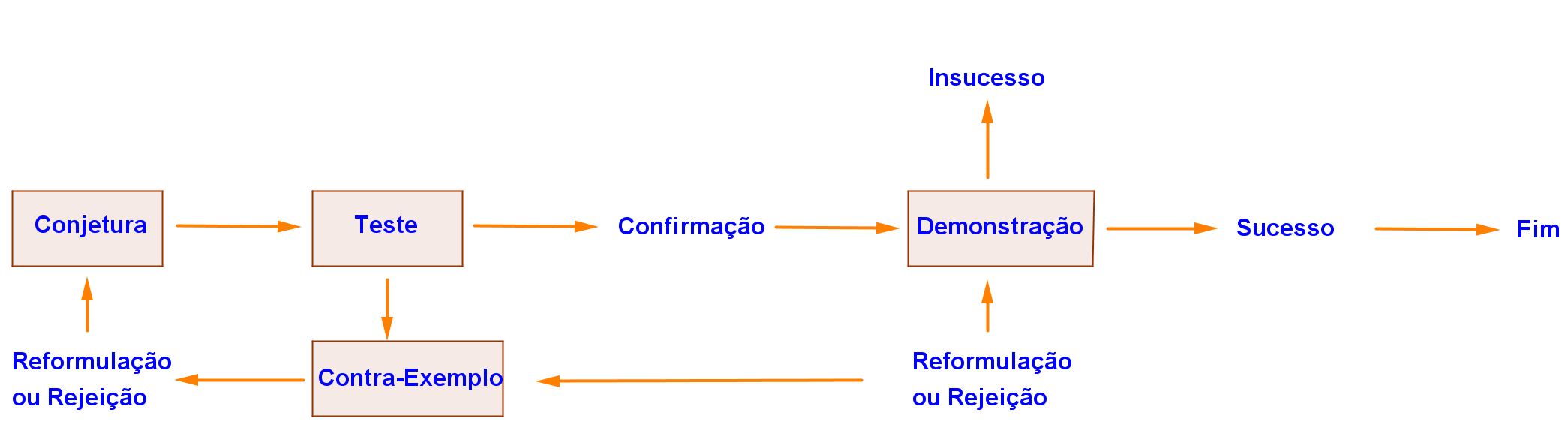
Neste processo que pode ser iniciado recorrendo a um raciocínio abdutivo na transição do raciocínio indutivo para o dedutivo outros objetivos ocultos se tornariam alcançáveis, tais como: tornar clara a distinção entre axiomas, conjeturas, teoremas e corolário; relacionar conceitos e resultados em Geometria; e predispor os estudantes para a utilidade da Geometria através de um verdadeiro exercício de autonomia e perseverança.

A implementação e análise da tarefa enquadram-se numa investigação qualitativa com caráter interpretativo. A escolha teve por base: a fonte direta dos dados recolhidos ter sido em ambiente natural (a sala de aula de matemática); um dos investigadores ter sido o agente na recolha desses mesmos dados (observação direta); e os dados recolhidos serem essencialmente de carácter descritivo (produções dos alunos) (Bogdan & Biklen, 2013). As turmas A e B tinham 32 e 30 estudantes respetivamente. Os estudantes trabalharam a pares. Nas duas turmas os grupos de estudantes anotaram as suas descobertas e, no fim da aula, todos os registos com as conjeturas a que tinham chegado foram recolhidos para posterior análise. Para analisar os dados fez-se uma codificação obtida na revisão do conjunto de dados, com a finalidade de determinar padrões que descrevessem características particulares do fenómeno estudado, e a análise de conteúdo suportada pelo desenvolvimento dos procedimentos de categorização dos dados (Bogdan & Biklen, 2013).

Para a realização deste estudo foram elaboradas duas tarefas, aplicadas em sala de aula em dois momentos diferentes, dezembro de 2013 e março de 2014.

Os polígonos propostos para as duas tarefas foram o triângulo médio e o quadrilátero médio, um para cada uma das duas turmas. Na Figura 2 encontra-se o enunciado da tarefa implementada após a apresentação da definição dos polígonos referidos:

A tarefa relacionada com o quadrilátero médio possuía um enunciado análogo ao apresentado na Figura 2.

Nesta contribuição vamos discutir o potencial oferecido por um AGD não só no apoio aos processos conjeturar mas também na mediação do significado matemático de conjeturas no contexto da Geometria.

A tarefa e o Geogebra

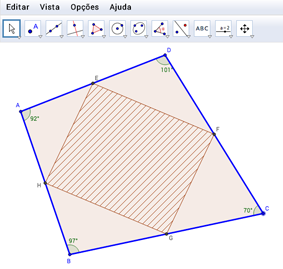
Numa primeira fase o professor apresentou a definição de polígono médio de um dado polígono, em particular, do triângulo e do quadrilátero. Estas definições eram de simples entendimento pelo que, com apenas dois exemplos, foi possível prosseguir para a construção no Geogebra de vários polígonos da família do polígono pedido. Os estudantes foram convidados a descobrir autonomamente propriedades desse polígono que lhes era totalmente desconhecido. Daqui, através da intuição e da experimentação, foram surgindo conjeturas. Para facilitar as múltiplas tentativas os estudantes criaram uma ferramenta para representarem mais rapidamente os polígonos médios e outros foram alterando o triângulo inicial movendo os seus vértices (ver na Figura 3 o applet clicando na própria imagem).

 Figura 3. Quadrilátero Médio

No momento da exploração e elaboração das conjeturas, o papel do professor foi fundamental para orientar as investigações dos estudantes, quer para conforto destes quer para conseguir alcançar os ob jetivos traçados. Na fase seguinte o professor desafiava-os a verificarem a veracidade da conjetura apresentada, em diferentes polígonos iniciais, a partir dos quais eram representados os polígonos médios, onde poderiam encontrar um contraexemplo para conjeturas falsas ou a verificação em todos os exemplos testados. Na verificação deste último caso, tal como defende Villiers (2003), os AGD ajudam a despertar nos estudantes “uma curiosidade mais prolongada pedindo-lhes para explicarem porquê” (p. 41) e, consequentemente reconhecer rapidamente “que a verificação indutiva/experimental apenas confirma; não produz conhecimento profundo, nem compreensão” (p. 41).

Na proposta de uma tarefa deste género o professor tem de ter a consciência de que as descobertas provenientes destas investigações podem não ser do seu próprio conhecimento. Tal como referem King e Schattschneider (1997) o professor tem de estar preparado para descobertas inesperadas e, tal como aconteceu com Boehm (1997), ter de dizer, por vezes, “não sei, vou ver se descubro e depois digo-te” (p. 72).

O início da exploração desta tarefa foi muito difícil para estes estudantes que não estavam habituados a produzir este tipo de conhecimento de forma autónoma. Contudo, à medida que as conjeturas iam surgindo, a motivação revelava-se crescente e as descobertas aumentavam significativamente.

As conjeturas surgiram ao longo destas duas horas. Nas duas turmas produziram-se mais de 20 conjeturas e cerca de metade resultaram em teoremas. Na procura incessante das conjeturas, os estudantes tentavam relacionar conceitos (ainda que óbvios) que tinham aprendido com as propostas de atividades na iniciação ao Geogebra, tais como: o ponto de Fermat, a reta de Euler (Figura 5), os polígonos cíclicos (Figura 4), os triângulos órticos, o teorema de Napoleão, entre outros.

Figura 4. Conclusões da Ana e da Marta sobre Polígonos Cíclicos

A definição de polígono cíclico permite concluir que todo o polígono regular é cíclico, contudo o grupo Carla e Andreia necessitou de várias experiências com o Geogebra para o seguinte registo: “Se para obtermos um polígono cíclico necessitamos que os seus vértices estejam inscritos numa circunferência, então todo o polígono regular é cíclico”.

Para além dos conceitos anteriormente apresentados, considerando [A’B’C’] o triângulo médio de um dado triângulo [ABC](*)  e [D’E’F’G’] o quadrilátero médio de um dado quadrilátero [DEFG], os estudantes conjeturaram, entre outras conclusões, que:

• os triângulos [ABC] e [A’B’C’] são semelhantes de razão 2:1;
• o circuncentro do triângulo [ABC] é o ortocentro de [A’B’C’]. O grupo Cátia e Soraia registou: “o ortocentro do triângulo médio coincide com o circuncentro do triângulo original”;
• qualquer triângulo tem a mesma reta de Euler que o triângulo médio (ver Figura 5);

Figura 5. Construção, no Geogebra, das Retas de Euler (Coincidentes) pelo Grupo Ana e Xavier

• os quadriláteros [DEFG] [D’E’F’G’] são semelhantes de razão 2:1;
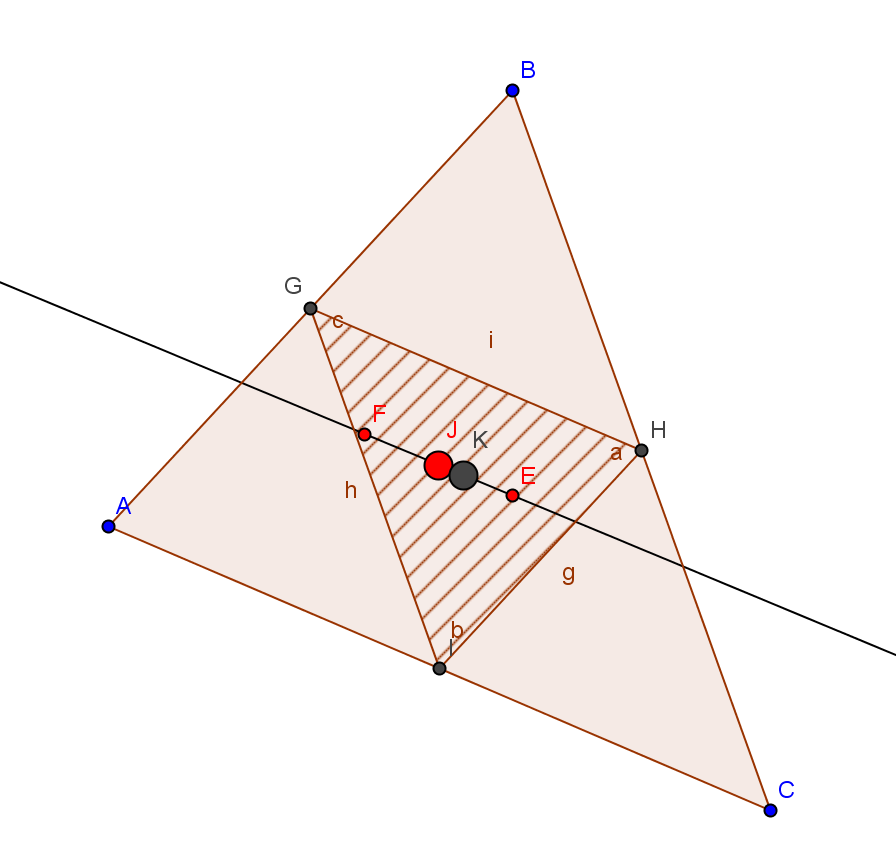
• o quadrilátero médio de qualquer quadrilátero é um paralelogramo (Figura 6).

Figura 6. Estratégia da Joana e da Sofia na Exploração dos Quadriláteros Médios

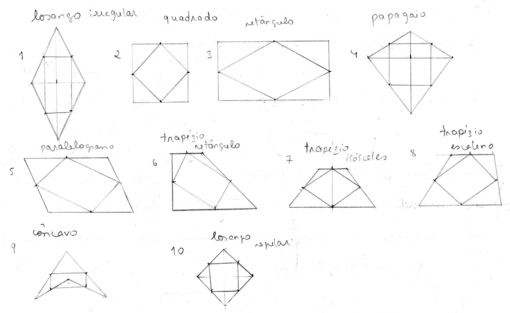
Os caminhos percorridos diferiam entre os pares de estudantes, uns procuravam propriedades em polígonos específicos (ver Figuras 6 e 7), outros estudavam na generalidade e, através da deslocação dos seus vértices, obtinham outros triângulos ou quadriláteros e observavam a transformação dos respetivos polígonos médios. Esta última estratégia foi também apontada por Jones (1998 citado por Candeias, 2005) com alunos do Ensino Básico onde estes modificavam “a figura até ficar com a forma pretendida, em vez de fazerem a respectiva construção” (p. 22). Apesar do caminho escolhido, a intuição baseada no que o olho conseguia ver esteve sempre na base de qualquer conjetura.

Figura 7. Estratégia da Daniela e Marta na Exploração dos Triângulos Médios

Ao longo desta exploração verificou-se que os estudantes produziam teoremas que estavam diretamente relacionados, por exemplo, descobriam a relação entre as áreas e os perímetros dos dois polígonos, o inicial e o médio, mas tinham dificuldade em relacionar estas conclusões com a razão de semelhança que também tinham determinado.

No final reuniram-se todos os teoremas que os estudantes haviam descoberto e propusemos o seu agrupamento por temas. Desta forma algumas conexões entre as descobertas realizadas fizeram sentido para os grupos que concluíram que, uma grande parte das suas descobertas estava relacionada com a semelhança de figuras, outros resultados surgiam isolados ou em pequenos grupos. Neste agrupamento as noções de teorema, corolário e postulados, tornaram-se essenciais e significativas.

  Reações à tarefa e ao uso do Geogebra

O Geogebra não demonstra mas ajuda a espelhar a forma de demonstrar e adequa-se plenamente na perfeição a este tipo de tarefas de descoberta e investigação. Repare-se que numa primeira fase as potencialidades destes programas de computador produzem evidências empíricas suficientes para convencer o investigador da veracidade de uma conjetura tornando a Geometria mais divertida (Bennett, 2003). O desenvolvimento desta atividade seria muito difícil se as construções fossem realizadas com recurso à régua e compasso pois demoraria muito tempo até se conseguir desenhar todos os casos possíveis.

No início os estudantes necessitaram de algum apoio pois tinham começado uma tarefa de investigação autónoma à qual não estavam habituados, o que lhes causava algum desconforto pela incerteza do caminho a percorrer. A ideia que tinham da matemática era a de um formalismo próprio de uma área disciplinar milenar cujas descobertas não lhes estavam acessíveis pois, nas suas mentes, eram apenas aprendizes da matemática e não investigadores.

No final da atividade o feedback foi claramente positivo pela generalidade dos estudantes de onde destacamos o registo que o grupo Ana e Francisca fez, escrevendo:

Na nossa opinião a ferramenta Geogebra mostrou-se bastante útil por diversos motivos: facilidade, rapidez e exatidão na construção das figuras e na aplicação de várias ferramentas nas figuras (tal como a amplitude dos ângulos, ou a bissetriz, ou o ponto médio entre outros); pela dinamização das figuras – estas podem ser alteradas, rodadas, ampliadas, ou seja, um sem número de possibilidades que, no papel levariam a muitas construções; facilita o trabalho em grupo pois ambas podemos experimentar, simultaneamente, a mesma ferramenta.

Os estudantes afirmaram que o momento de descoberta foi muito interessante e de alguma reflexão sobre a ferramenta utilizada e a tarefa de investigação. Alguns consideraram ainda que com o Geogebra enfrentam o erro e as conjeturas falsas de um modo positivo, por conseguirem facilmente corrigir erros, construir rapidamente outras figuras ou alterar partes da mesma.

 Conclusão

A tarefa de investigação proposta aos estudantes do 3.º ano da Licenciatura em Educação Básica proporcionou-lhes um momento de produção matemática onde puderam testar as suas próprias conjeturas e ideias de uma forma mais participativa no seu próprio processo de aprendizagem. No 2.º ano da LEB estes estudantes frequentaram uma unidade curricular com 60h de Geometria e os docentes puderam constatar que as suas experiências escolares prévias, com Geometria, consistiram predominantemente na utilização de fórmulas algébricas para a resolução de problemas geométricos, e no reconhecimento e memorização de propriedades de objetos geométricos. Esta realidade tinha como consequência a ausência de compreensão dos conceitos, factos e conexões entre os diversos temas. O recurso a representações visuais foi um auxílio importante para a compreensão de alguns factos que até agora lhes tinham sido apenas apresentados, situações tão simples como a soma dos ângulos internos de qualquer triângulo ser sempre igual a 180º.

Nas tarefas realizadas com o Geogebra, o momento inicial foi marcado pela ausência de autoconfiança por parte dos pares de estudantes no desenvolvimento da exploração proposta. O apoio do professor revelou-se fundamental para que, numa fase posterior, os grupos encontrassem o seu percurso de forma autónoma. Deste modo foi possível observar que os caminhos adotados divergiam entre os grupos.

Os grupos de trabalho revelaram um forte entusiasmo na descoberta de novas hipóteses denotando dificuldade em destacar aspetos que não fossem característicos da própria figura, tais como, “a soma dos ângulos internos do triângulo inicial e do triângulo médio é 180º”.

Todas as reações registadas pelos grupos de estudantes apontaram aspetos benéficos da utilização deste programa e destas experiências que se podem separar em dois grupos: o dos afetos e o da aplicabilidade. Na aplicabilidade deste programa realçam a compreensão das propriedades dos objetos geométricos e de relações entre estes. Outro grupo sublinha o carater dinâmico do programa referindo que confere rigor às construções e reduz, por isso, a sua morosidade e complexidade, caso tivessem de as construir recorrendo a materiais de desenho. Da observação direta constatou-se o desenvolvimento de uma interação entre os pares que, na maioria dos casos, foi benéfica para o grupo: permitiu melhorar o vocabulário específico utilizado; a capacidade de argumentação e o raciocínio sobre as figuras geométricas.

Em suma, a utilização do Geogebra teve não só o propósito de estimular uma aprendizagem e compreensão de aspetos da matemática, como permitiu elevar a autoconfiança dos estudantes, a autoestima e a predisposição para o desenvolvimento de tarefas de investigação em matemática onde a Geometria, por ser uma área particularmente fértil, pode ser um meio eficaz para atingir esse fim.