1. Sobre a proposta metodológica
A experiência docente(*) da autora deste relato, ministrando diversos assuntos de matemática no ensino superior a partir da grandeza vetorial, influenciou majoritariamente para o desenvolvimento de uma proposta metodológica para a matemática do ensino médio através do conceito de vetor, elegendo-o como aspecto básico e primordial para a maioria dos conteúdos subsequentes.
As inquietações com o currículo fragmentado brasileiro (PCN, 1999) e a aprendizagem ineficaz dos alunos da escola secundária (Nasser, 2009; Rezende, 2003) propiciaram ressignificar os conteúdos de matemática na prática letiva, recorrendo ao conceito de vetor como base e à Geometria Vetorial como estrutura. A utilização dos vetores como uma via de geometria dinâmica para dar sentido aos diversos conteúdos do ensino médio transformou-os ao olhar do professor, apresentando-os a partir de outras características.
Os estudos apresentados por Bittar (2013) justificam a utilização dos vetores nos programas curriculares desde o 4o ciclo do ensino fundamental, assim como ocorre nas escolas francesas. A referida autora mostra, através do Registros das Representações Semióticas de Duval, que a Geometria Vetorial configura-se para o aluno como ganho de mais uma ferramenta na resolução de problemas já conhecidos quando é apresentada inicialmente como um ente geométrico para resolver problemas de geometria. Ademais, ela aponta estudos sobre as dificuldades dos alunos na aprendizagem do conceito de vetor.
A iniciativa para elaborar, desenvolver e pôr em prática uma proposta metodológica para o ensino médio originou-se há dez anos como resultado de reflexões acerca dos processos de ensino e aprendizagem dos alunos. O conhecimento matemático e a vivência profissional da autora deste relato foram propulsores para a aplicação prática e experimental de uma metodologia de ensino em uma escola pública e federal do Rio de Janeiro, Brasil. No ano de 2006, o ensino médio do referido colégio sofreu mudanças curriculares baseadas na proposta que será explicitada. O objetivo principal era permitir uma associação consistente entre os assuntos estudados na escola, reconfigurando os conteúdos de matemática das três séries do ensino médio, partindo do conceito de vetor, e promovendo uma forma de relação que denominou-se de ‘fluida’ neste trabalho, a qual será explicada posteriormente na Mídia 1.
Entre os anos de 2006 e 2013, inclusive, o engendramento de conteúdos de matemática foi sendo cultivado, incentivado, aplicado e reformulado com as turmas de ensino médio do referido colégio, de forma experimental, observadora e analítica, constituindo-se em uma Proposta Metodológica de Ensino. Primeiramente, a aplicação deu-se na 1a série e, posteriormente, estendeu-se às 2a e 3a séries. Nesse período, as versões da proposta foram sendo testadas e modificaram-se conforme observação e reflexão das respostas dos alunos, postos em atividades sob uma ótica investigativa. A aplicação da proposta, seus resultados e modificações serão explicitados nas seções seguintes.
Vale ressaltar que a proposta – em sua versão do ano de 2011 – foi utilizada como referência em pesquisas do Projeto Fundão(*) sobre a transição do ensino médio para o superior. Os estudos de Nasser, Souza e Torraca (2012) mostram que esta proposta é uma abordagem metodológica que colabora minimizando as dificuldades dos alunos ingressantes na disciplina de Cálculo I e a destacam como sendo a possibilidade de um currículo em espiral, no qual os conteúdos são constantemente revisitados (p. 16).
Para fundamentar a proposta, buscou-se valorizar a visão geométrica dos alunos, incentivando esse olhar aos assuntos abordados em todo o ensino médio, inclusive àqueles nos quais a interpretação tradicionalmente explorada é exclusivamente algébrica. De maneira concisa, pode-se afirmar que a utilização do conceito de vetor no início da 1a série do ensino médio proporciona, dentre outros:
-
A construção da representação gráfica de uma circunferência, através do conceito de módulo de vetor.
-
A possibilidade de explorar a geometria euclidiana no plano cartesiano.
-
A utilização das transformações no plano para o ensino de trigonometria, promovendo: a visualização e compreensão dos arcos no círculo a partir da rotação de um vetor em torno da sua origem; a utilização da geometria euclidiana como uma ferramenta para o estudo da trigonometria; a determinação da equação da reta a partir da translação de um ponto segundo um vetor; a simetria central e axial como ferramentas de localização cartesiana dos vértices de polígonos regulares centrados na origem.
-
A determinação da função afim a partir do estudo da equação da reta.
-
A constituição da expressão algébrica de uma determinada função ou de uma cônica, a partir de sua designação mais simples, através do conceito da translação.
-
A translação de gráficos de funções ou de cônicas.
-
O estudo da geometria espacial – tradicionalmente explorada apenas por suas medidas de comprimento, superfície e capacidade – a partir do conceito de vetor em lR3 .
-
A visualização geométrica e espacial dos planos – cuja representação algébrica constitui um sistema linear – através das relações entre os vetores normais, principalmente nos casos em que o sistema não é possível e determinado.
-
A conceituação de matrizes como um conjunto de vetores linha (ou coluna), propiciando a construção de significados de algumas operações matriciais que se equivalem às operações vetoriais já conhecidas(*) .
-
O auxílio da geometria plana e dos vetores em lR2 para o estudo de números complexos e suas representações geométrica e trigonométrica.
Como um meio direto de visualizar a proposta de interligação da maioria dos conteúdos de matemática do ensino médio, apresenta-se um fluxograma, no qual é importante observar alguns detalhes, tais como:
-
O video apresenta uma forma de relação entre os conteúdos, na qual utilizou-se: setas de um e dois sentidos; objetos (conteúdos); cores que se identificam nas setas e objetos.
-
Os conteúdos estão se relacionando e mostrando graficamente, através das setas, as possibilidades de ‘caminhos’ a percorrer, possibilitando ao professor múltiplas alternativas de planejamento didático.
-
Acerca de uma visão geométrica do fluxograma, pode-se dizer que o único ponto de partida é o objeto ‘Vetores’ e os pontos de chegada (finais) são os objetos ‘Geometria Espacial’, ‘Números Complexos’ e ‘Gráficos’.
-
Todos os conteúdos selecionados do ensino médio – e que fazem parte do fluxograma – estão em um processo de relação com outros conteúdos, articulando-se de forma fluida e contínua (exceto os pontos finais, indicados anteriormente).
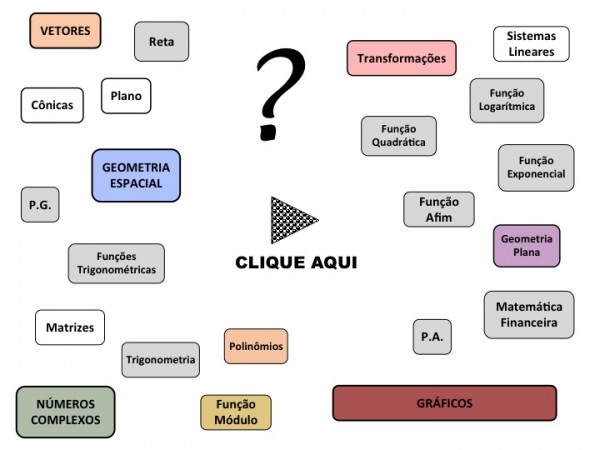
Mídia 1 – Proposta fluida de associação de conteúdos a partir do conceito de vetor
(P.A.: Progressão Aritmética e P.G.: Progressão Geométrica)
Com relação à abrangência dos conteúdos do fluxograma, não foram contemplados tópicos de combinatória, probabilidade, estatística, lógica e outros referentes à matemática discreta. O fluxograma foi elaborado apenas com os temas que propiciam associação, os quais representam em torno de 84% do currículo do ensino médio, tomando-se por base a média de conteúdos indicados pelas normas de ensino do Brasil. Isso deve-se ao fato de que os assuntos referentes à matemática discreta não têm relação com as características geométricas, algébricas e numéricas que constituem o vetor.
A proposta constitui-se como uma possibilidade de engendramento de conteúdos sobre a qual já foi construído um material didático com tarefas de matemática para atividades em sala de aula. Para ilustrar de forma pedagógica a concepção epistemológica adotada, encontra-se um exemplo na próxima seção.
2. Um breve recorte da Proposta Metodológica de Ensino
Apresenta-se uma ínfima parte da proposta para tentar explicitar o engendramento de conteúdos no ensino da Trigonometria no Círculo a partir do conceito de vetor.
Recorrendo ao fluxograma (Mídia 1), é possível perceber que os vetores podem conectar-se aos estudos das Transformações no Plano, nomeadamente: translações, simetrias, rotações e homotetias. No âmbito das Rotações do Plano, conceitua-se como: uma transformação que produz um giro de um objeto em torno de um centro fixo, segundo um ângulo determinado. Inicialmente, considera-se esse objeto como sendo um vetor v, representado pela Figura 1.
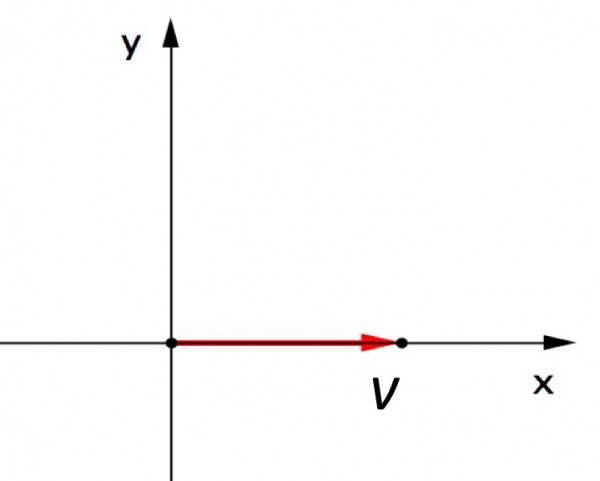
Figura 1 – Vetor centrado na origem do plano cartesiano e ângulo de inclinação de medida zero grau (com o eixo OX positivo).
A Figura 2 representa a rotação de v, em torno da origem, segundo um ângulo θ. O resultado será um vetor u, de modo que a extremidade do vetor v descreva um arco de medida θ.
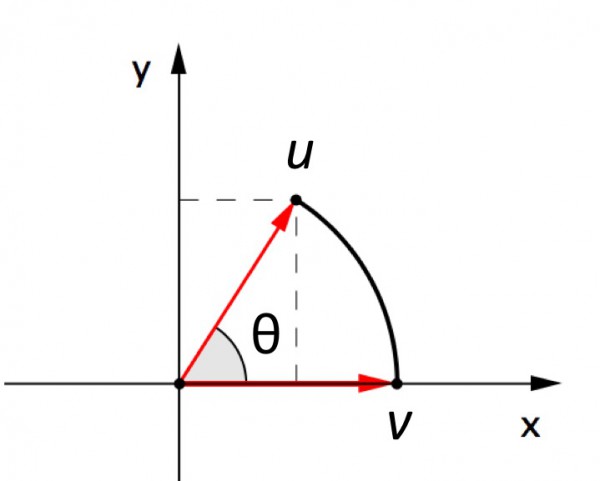
Figura 2 – Rotação do vetor v em torno da origem, segundo o ângulo teta.
Ao considerar o ângulo θ = 360o, a rotação do vetor v, em torno da origem, segundo um ângulo de 360o, faz com que a extremidade do vetor descreva uma circunferência de raio de medida |v|. Isto é, a extremidade do vetor percorreu uma distância que representa o comprimento da circunferência de centro em O e raio |v|, ou seja, 2π|v|, conforme a Figura 3.
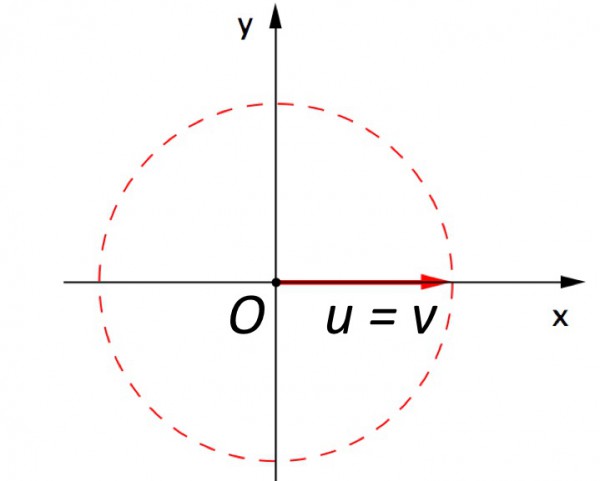
Figura 3 – Rotação do vetor v em torno da origem, segundo o ângulo de 360 graus.
Partindo dessa ideia, o professor tem a possibilidade de explorar vários conceitos: o comprimento do arco, utilizando-se de uma simples regra de três; o círculo trigonométrico, quando o vetor é unitário; os arcos múltiplos, através de rotações iguais (12 de 30o ou 8 de 45o ou 6 de 60o ou 4 de 90o ou 2 de 180o); as noções de seno e cosseno dos arcos sem recorrer à fórmulas ou regras prontas, que indicam o caminho da memorização para os alunos (Azevedo, 2013) e (Assemany, Silva, Arquieres, Marques & Barino, 2014). Para isso, deve-se determinar as novas coordenadas do vetor resultante ao variar o ângulo de rotação.
Para exemplificar alguns desses conceitos, sugere-se uma atividade indicada para a introdução da Trigonometria no Círculo, uma vez que os pontos divisores de uma circunferência são extremidades dos vetores canônicos e suas coordenadas são o seno e cosseno dos arcos formados com o eixo positivo.
2.1. Atividade sugerida
Considere uma circunferência determinada pela rotação do vetor (1,0) sobre a origem do plano cartesiano, segundo um ângulo de 360o. Esboce seu desenho no papel milimetrado e divida-a em 12 partes iguais, a partir da interseção com o eixo OX. Em seguida, faça o que se pede:
a) Indique a medida em graus (no sentido positivo) do arco determinado por cada ponto divisor e a origem da circunferência.
b) Localize os pontos divisores dos seguinte arcos: π/6 rad , 2π/6 rad, 3π/6 rad, 4π/6 rad, 5π/6 rad , 6π/6 rad, 7π/6 rad, 8π/6 rad, 9π/6 rad, 10π/6 rad, 11π/6 rad e 12π/6 rad. O que você observa?
c) Observe os pontos divisores dos seguintes arcos: π/6 rad , 5π/6 rad, 7π/6 rad e 11π/6 rad. Quais as relações geométricas que você identifica entre estes arcos?
d) Observe os pontos divisores dos seguintes arcos: π/3 rad , 2π/3 rad, 4π/3 rad e 5π/3 rad. Quais as relações geométricas que você identifica entre estes arcos?
e) Determine as coordenadas dos vetores cujas extremidades são os arcos π/6 rad, 5π/6 rad , 7π/6 rad, 11π/6 rad.
f) Determine o seno dos ângulos cujas medidas dos arcos são: π/6 rad, 5π/6 rad , 7π/6 rad, 11π/6 rad. (Utilize o triângulo retângulo que se forma pelo vetor e sua projeção ortogonal no eixo.)
g) Determine o cosseno dos ângulos cujas medidas dos arcos são: π/6 rad, 5π/6 rad , 7π/6 rad, 11π/6 rad. (Utilize o triângulo retângulo que se forma pelo vetor e sua projeção ortogonal no eixo.)
h) Observe suas respostas aos itens f) e g) e compare com as coordenadas indicadas no item e). O que você pode inferir?
i) Discuta com os colegas e o professor sobre suas reflexões.
Essa atividade tem o objetivo de conduzir o aluno às seguintes percepções:
-
Identificação dos vetores simétricos em relação aos eixos e/ou origem.
-
Reconhecimento de que cada uma das 12 partes de 30o representa uma fração de π/6 rad, o que auxilia na determinação da medida do ângulo em radianos, assim como as 8 partes de π/4 rad ou 6 partes de π/3 rad, etc.
-
Estímulo à geometria analítica, especialmente ao plano cartesiano e aos recursos da geometria plana e trigonometria no triângulo retângulo, para o desenvolvimento de conceitos e habilidades em matemática e nos conteúdos posteriores.
-
Correlação das coordenadas dos vetores aos valores do seno e cosseno dos arcos, sem recorrer a fórmulas e regras de sinais.
3. Implementação e Constituição da Proposta Metodológica de Ensino
No ano de 2006, a autora deste relato deu início à implementação da primeira versão da Proposta Metodológica de Ensino – PME nas turmas de 1a série do ensino médio do colégio(*) público brasileiro referido anteriormente, atuando como professora. A cada ano, alguma inserção ou adaptação ou alteração na proposta era feita por ela, de acordo com o feedback dos alunos em sala de aula e/ou pesquisas pontuais. Contudo, nem sempre a autora atuou como professora regente de todas as turmas. Quando isso acontecia, ela mantinha a função de coordenadora da série, fazendo um acompanhamento semanal com os professores e orientando-os para que as aulas estivessem conforme a PME.
A tabela a seguir explicita o que foi produzido em cada ano de implementação da PME.
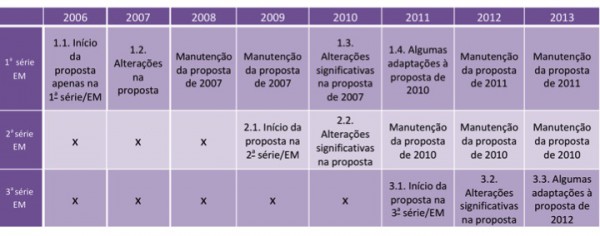
Tabela 1 – Estrutura da aplicação e reformulação da proposta
Relativamente às pesquisas realizadas no período de implementação e constituição da PME, destacam-se:
-
Em 2011 - Assemany e Azevedo (2011) mostram o trato puramente geométrico na determinação das raízes complexas de um número complexo, abordado com os alunos da 3a série do ensino médio.
-
Em 2012 – Nasser e outros (2012) apontam que os alunos egressos do colégio C tiveram um bom aproveitamento, em comparação com outras escolas públicas e privadas do Rio de Janeiro, quando defrontados com situações-problema referentes ao Cálculo.
-
Em 2013 – Azevedo (2013) apresenta alguns resultados sobre a PME com estudantes do ensino médio do colégio C, que serão destacados no próximo tópico. Assemany e Harab (2013) relatam uma parte da PME, nomeadamente o ensino de números complexos. Assemany, Nasser, Alves, Azevedo e Torraca (2013) descrevem a PME relativa à 1a série do ensino médio. Assemany e outros(*) (2014) categorizam os obstáculos epistemológicos dos alunos do colégio C e os comparam com os de estudantes do ensino superior, conforme a próxima seção.
Destacar-se-á os principais tópicos que constituíram cada versão da proposta:
1.1. A primeira versão era bem parecida com a PME. No entanto, alguns engendramentos ainda não eram tão definidos e bem relacionados. Por exemplo: A equação da circunferência pode ser determinada apenas pelo simples fato do módulo do vetor ser igual ao raio, sem recorrer à fórmula. Essa é uma conclusão óbvia para os alunos que estudaram vetores, pois basta utilizar esse conceito para sua dedução, ou de forma literal ou com os valores do próprio exercício.
1.2. A segunda versão foi alterada pelo motivo anterior apresentado. Situações como essa aconteceram em sala de aula e propiciaram à professora (autora deste relato, idealizadora e desenvolvedora da PME) a repensar as situações que deveriam ser incluídas, retiradas, reconectadas, revistas, ressignificadas e reorganizadas. Um exemplo da versão de 2007, que não estava na versão de 2006, foi o Estudo da Reta antes da Função Afim, a qual não se configurou como sendo y = ax + b por via da memorização. Para determinar uma reta, os alunos perceberam (primeiro visualmente e depois vetorialmente) que bastava transladar um ponto dado, segundo um vetor (que tinha a direção da reta), pois assim determinavam um outro ponto da reta. Para determinar um terceiro ponto, fariam isso novamente, sucessivas vezes, até determinarem a equação vetorial da reta, que poderia conduzir a qualquer forma de equação, inclusive à reduzida (afim, se y for a variável independente).
1.3. A terceira versão continha alterações significativas. Foram incluídas as transformações de translação, rotação, simetria e homotetia com o apoio do software GeoGebraTM; a análise das funções Afim e Quadrática foi feita com um olhar amplo, no qual era possível determinar áreas e translações; resolver equações/inequações graficamente; e a construção de suas representações gráficas levou em conta suas propriedades geométricas. Embora o conceito de vetor estar presente desde a versão de 2006, a Geometria Vetorial passou a ser estabelecida na PME somente a partir da versão de 2010. Foi o amadurecimento com as versões anteriores da proposta que promoveu a elaboração da primeira versão para a 3a série (3.1), e que também possibilitou que a versão de 2010 da 2a série fosse ligeiramente desconstruída.
1.4. A quarta e última versão da proposta da 1a série foi composta apenas de algumas adaptações à versão de 2010, em que a Geometria Vetorial ficou conceituada como uma abordagem vetorial que permite e promove integração de conteúdos.
2.1. A primeira versão da 2a série buscou manter o compromisso de ensino das funções e seus gráficos pela Geometria Vetorial, que deveria ser construída pelo professor regente, que não era a autora neste ano. A proposta na 2a série ainda era experimental, uma vez que o foco maior concentrava-se na 1a série, cuja proposta já estava em sua segunda versão reelaborada.
2.2. A segunda versão da 2a série teve um foco menor na geometria, uma vez que notou-se certa fragilidade algébrica nos estudantes que chegavam à 2a série. Contudo, aproveitou-se para dar ênfase aos tópicos da matemática discreta (combinatória, probabilidade, estatística, matemática financeira) e às funções algébricas reais – gráficos, equações e inequações.
3.1. A primeira versão da 3a série contemplou todos os conteúdos remanescentes do ensino médio, a saber: números complexos, polinômios, matrizes e determinantes, sistemas lineares, cônicas, geometria espacial, estudo de vetores, retas, planos em lR3, esfera e superfície esférica. Para confeccionar a proposta, alguns desses conteúdos foram explorados pela Geometria Vetorial, como os números complexos (Assemany & Azevedo, 2011), a geometria espacial – especificamente os prismas, juntamente com os sistemas lineares e as equações dos plano – as matrizes e a esfera.
3.2 e 3.3. A segunda versão da 3a série apresentou-se mais consistente por ter o resgate às transformações no plano por via das matrizes, possibilitando que os alunos pudessem elaborar um mini projeto matemático de um simulador de movimentos por meio da translação e rotação de vetores, conforme apresentado por Sandres, Correa, Nedjah e Mourelle (2012). Além disso, os polinômios receberam uma abordagem que justificasse a função polinomial, dando mais sentido ao seu estudo, e os outros conteúdos acabaram por engendrar-se naturalmente, acomodando-se e contribuindo para a construção de uma Proposta Metodológica de Ensino para as turmas de 1a, 2a e 3a séries, representada pelo fluxograma da Mídia 1.
Como consequência da prática docente e implementação da PME, realizaram-se estudos sobre o ensino da matemática e pautados em experiências próprias, a saber: classe de estudantes do ensino médio, orientandos de monografias de final de curso universitário e grupos de discussão acerca do tema. Referente às investigações nestes oito anos de aplicação prática da abordagem didática, serão apresentadas apenas duas pesquisas diferentes, evidenciando-se alguns dados recolhidos e os respectivos resultados obtidos.
4. Alguns resultados de investigações
Em sua monografia(*), Azevedo (2013) defende que a presença dos vetores na estrutura curricular do ensino médio é um diferencial positivo para estudantes na transição para o ensino superior. Esta pesquisa apoiou-se em PCN (1999) como referencial teórico e o trabalho de campo deu-se através de métodos qualitativo e quantitativo em quatro etapas: i) acompanhamento semanal das aulas de matemática em uma turma de cada série do ensino médio nos anos de 2010 e 2011, e diálogos com os professores regentes destas turmas; ii) participação na elaboração de atividades e avaliações para as turmas acompanhadas; iii) aplicação de questionários a grupos de alunos e ex-alunos do colégio C; iv) análise dos dados.
Para analisar as contribuições da abordagem vetorial, Azevedo (2013) descreveu cautelosamente a proposta metodológica aplicada à 1a série do ensino médio e apresentou alguns reflexos nas séries posteriores, como a utilização de softwares de geometria dinâmica, nomeadamente o GeoGebraTM, na construção de significados algébricos por intermédio do conceito de vetor. Os objetos de recolha de dados apresentavam-se em forma de questionários a dois grupos: os concluintes do ensino médio e os que ingressaram no ensino superior em alguns cursos de ciências exatas. Conforme Azevedo (2013), a pesquisa mostrou que os alunos de ambos os grupos se tornaram mais perspicazes a deduzir fórmulas, ao invés de memorizá-las, e a representar de diversos modos os mesmos objetos, através de vários olhares em diferentes momentos do ensino médio, por consequência da estrutura interconectada dos conteúdos: (…) a abordagem baseada na Geometria Vetorial parece oferecer um preparo melhor para os alunos na transição do Ensino Médio para o Ensino Superior (p. 67).
O estudo quantitativo indicou, dentre outros, que 85% dos alunos utiliza os conceitos de vetores em alguma outra área do conhecimento. Com relação à avaliação de seu próprio ensino, 77% atribuiu o valor ‘ótimo’ ou ‘muito bom’, 18% considerou ‘bom’, 5% indicou ‘regular’ e ninguém optou por ‘ruim’. A investigação qualitativa das respostas dissertativas do questionário sobressaltou o destaque positivo dos alunos quanto ao método de ensino diferenciado, pois permitiu adquirir um olhar amplo sobre o conteúdo e obter diversas ferramentas para a resolução do mesmo problema.
Como consequência dos estudos de Azevedo (2013), deu-se início a outra investigação acerca da estrutura curricular do ensino médio através do registro das representações semióticas em educação matemática, desenvolvida por Assemany e outros (2014). Apoiados na metodologia dos obstáculos epistemológicos de Bachelard, os autores realizaram uma investigação na qual buscaram evidenciar os ‘entraves à aprendizagem’ através da resolução de questões de matemática do ensino médio. Os sujeitos da pesquisa foram alunos do ensino médio do colégio C e do ensino superior dos cursos de Matemática e Física de uma universidade pública. Os resultados mostraram que os estudantes do ensino médio acertavam imediatamente, ou expunham vários recursos diferenciados para a resolução (Assemany e outros, 2014, p. 9). Já os alunos do ensino superior, tentavam algo que lhes fosse o tradicional, o conhecido, como uma fórmula, uma figura convencional, uma representação habitual (Ibidem, p.10). Esses dados apontaram para a escassa utilização de fórmulas e à priorização do raciocínio dos alunos do colégio C, em comparação com os da universidade.
Após a aplicação da proposta, surgiram algumas questões relacionadas à concepção da matemática escolar e à metodologia utilizada pelos professores em sala de aula. Para Carreira (2010), é essencial não desperdiçar as oportunidades de utilizar as conexões matemáticas na aprendizagem, integrando e propiciando a coerência dos conceitos: É impossível entender um conceito novo sem o relacionar com conceitos anteriores, sem elementos de mediação, sem analogias, pontes, metáforas, contextos, experiências (p. 1).
5. Considerações finais
De fato, acredita-se que esta não é a única forma de se propor o currículo da Geometria Vetorial do ensino médio. A proposta apresentada constitui-se como uma possibilidade de conexão de conceitos, mesmo que, em dada escola, cidade ou país, não haja correspondência com a abrangência de tópicos de matemática.
Com base no que se expôs neste relato, aspira-se contribuir para o ensino e a aprendizagem da matemática por meio da mudança de paradigmas que a proposta metodológica de engendramento de conteúdos promove, incentivando as pesquisas na área para que a geometria vetorial seja amplamente utilizada pelos professores e alunos da escola básica.
