INTRODUÇÃO
As tecnologias educativas permitem que os estudantes explorem, investiguem e resolvam problemas mais complexos que, até então, lhes eram inacessíveis (NCTM, 2000). Os ambientes de geometria dinâmica têm contribuído para o desenvolvimento do sentido geométrico e poderão desempenhar um papel fundamental na aprendizagem destes conteúdos (Laborde, 2000), ao permitirem “o acesso a modelos visuais poderosos a que os alunos, em especial os mais novos, não teriam acesso tão facilmente” (Breda, Serrazina, Menezes, Sousa, & Oliveira, 2011, p. 21). Estes autores acrescentam que “a tecnologia enriquece a extensão e a qualidade das investigações em geometria, ao fornecer um meio de visualizar noções geométricas sobre diferentes perspectivas” (p. 21). E, por outro lado, ao trabalhar-se com programas de geometria dinâmica “a aprendizagem dos alunos é auxiliada pela resposta que a tecnologia pode proporcionar” (idem).
Mas deverá a utilização sobrepor-se às ferramentas tradicionais como o compasso, a régua ou as miras? Que relação, ao nível concetual e procedimental, existirá entre estes instrumentos de aprendizagem da geometria? Neste estudo procuramos, assim, perceber qual o papel do programa GeoGebra na aula de Matemática quando se utilizam também, e de forma complementar, as ferramentas mais tradicionais e de que modo pode contribuir para a compreensão e aplicação do conteúdo isometrias do plano.
ENQUADRAMENTO TEÓRICO
As TIC no contexto educativo
Numa sociedade em contínua mutação, as evoluções tecnológicas, culturais e sociais influenciam claramente tudo o que se passa na Escola, em geral e, em particular, na sala de aula (Fey, 1984; Mendes, 1998; Tall, 1994). A tecnologia começa a apresentar-se como uma base e factor de comunicação (NCTM, 1991, 2000), potenciando a discussão e o confronto de ideias matemáticas (Fernandes, 2006). Também para Silva (2002), as tecnologias não são apenas meios ou instrumentos, mas são “contextos, linguagens e modos de comunicação, constituindo-se como janelas de oportunidades fundamentais para a organização progressiva do conhecimento” (p. 19). Devido à importância dada às tecnologias no mundo atual e à defesa intransigente da equidade numa sociedade democrática, dois dos seis princípios da educação matemática defendidos pela UNESCO são: equidade e tecnologia, articulando-se entre si para provocarem mais e melhor aprendizagem matemática. Por outro lado, o NCTM (2000) reitera esta necessidade ao defender que “o acesso à tecnologia precisa de se tornar numa outra dimensão educacional da equidade” (p. 14). Este organismo acrescenta ainda que “a tecnologia é essencial no processo de ensino e aprendizagem, dado que esta influencia a própria matemática que é ensinada e amplia, simultaneamente, a aprendizagem do estudante (NCTM, 2000, p. 14).
Por outro lado, a presença dos computadores na sala de aula cria um ambiente diferente na classe e, quando é fomentada uma aprendizagem experimental do conhecimento, esta passa pelo olhar atento, apoio individualizado e a orientação próxima do professor. Esta alteração de papéis dos estudantes e dos professores na sala de aula permite o levantamento de questões, uma aprendizagem pela descoberta e saberes mais significativos para todos os intervenientes (Fernandes, 2006).
Programas de Geometria Dinâmica e o GeoGebra
Nos estudos realizados por Fernandes (2006), com um programa de geometria dinâmica e outras ferramentas tecnológicas, conclui que, na classe, se desenvolve um clima mais favorável para a descoberta, a experimentação, a simulação de conceitos e a construção de novos saberes matemáticos.
Também o NCTM (2000) defende que os programas de geometria dinâmica, em especial o GeoGebra, permitem aos estudantes “focalizar a atenção para a capacidade de experimentar, reflectir, raciocinar e resolver problemas” (NCTM, 2000, p. 169) e providenciam um ambiente especial para se poder explorar relações, elaborar e testar conjecturas. Estas ferramentas tecnológicas oferecem oportunidades para se realizarem diferentes experiências com múltiplas representações, tais como: pictóricas, geométricas, numéricas, tabelares, gráficas, algébricas e manipulações que dinamizam o processo de aprendizagem e ensino da Matemática, permitindo o levantamento de determinadas questões e a consciencialização da necessidade de reflexão que importa aproveitar para incentivar a construção do conhecimento matemático. Seguindo esta perspectiva educacional vários investigadores (Fey,1984); Veloso, 1987, 1998; Ponte, 1991, 1997) defendem que os estudantes podem aprender mais matemática, pelo levantamento de novas questões e reflexões, proporcionando um tratamento mais profundo dos temas com a utilização apropriada da tecnologia, em particular dos programas de geometria dinâmica. O compromisso do estudante com as ideias matemáticas abstractas deve ser promovido, pois através destes programas enriquece-se o grupo e “a qualidade das investigações segundo múltiplos pontos de vista” (NCTM, 2000, p. 25).
Para Cannone e Socas (1998) a questão ideológica associada à acção educativa é também relevante quando se usa o computador na sala de aula, designadamente, os programas de geometria dinâmica. Assim, para se obterem resultados positivos na aprendizagem, quer em termos de motivação, quer em termos de maior compreensão dos conceitos, é imprescindível que o professor e o estudante pratiquem uma comunicação aberta e participativa. Segundo estes autores, neste contexto educativo, a atitude do professor passa de informador central para colaborador e orientador, permitindo também que o estudante saia da sua passividade para aprender a pensar e a participar.
Num estudo recente, realizado por Coelho (2013) a cinco estudantes e, na análise das respostas ao questionário final, constatou que existe “um alto grau de concordância por parte de todos os alunos sobre os benefícios da utilização do GeoGebra” (p. 222). Este investigador conclui ainda que “o software foi de fácil familiarização e que era: interessante; facilitador do trabalho com as transformações geométricas; promotor da autonomia dos alunos; facilitador do trabalho de grupo (ou em pares) e promotor da interação entre os alunos” (idem). Nesse mesmo questionário final e sobre a forma como o tópico tinha sido implementado, alguns estudantes referiram que “o programa os ajudou a perceber as isometrias, tornando a geometria menos complexa e mais divertida” (idem). Nesta experiência investigativa recente, Coelho (2013) refere ainda que o sucesso na resolução de uma tarefa no GeoGebra nem sempre assegurava um êxito similar quando a mesma era realizada em ambiente de “papel e lápis”, sendo um ponto crítico para os alunos com mais dificuldades. Registe-se ainda que “se a passagem do “papel” para o GeoGebra não constituía qualquer problema, o inverso não era verdade”, pois a capacidade de visualização e raciocínio espacial altera-se, evoluindo de forma natural nalguns alunos, mas noutros apresenta-se com menor proficiência. “Alguns alunos declaram ainda que, nomeadamente, o GeoGebra lhes permitia “criar” e possibilitava um melhor entendimento dos conceitos envolvidos (idem, p. 223).
Das pesquisas realizadas concluiu-se que vários autores consideram o GeoGebra uma mais valia, constituindo-se como uma ferramenta poderosa na resolução gráfica de problemas, permitindo aos alunos múltiplas abordagens para alcançarem um maior número de soluções, as quais lhes permitem a colocação de novas questões e aprendizagens no campo da geometria.
METODOLOGIA
Desenho metodológico
Atendendo às questões do estudo, foi adoptada uma abordagem de investigação qualitativa e interpretativa, seguindo as orientações de Bogdan e Biklen (1994), dado que a situação natural constitui a fonte dos dados, sendo necessário, num primeiro momento, descrever para analisar, posteriormente, os dados, valorizando-se o processo, bem como o produto e o resultado final. A entidade de análise é uma turma, através da qual se estuda o impacto da utilização do GeoGebra, complementarmente ao uso de ferramentas mais tradicionais, como a régua e o compasso, no estudo do conteúdo isometrias do plano, no 6º ano de escolaridade.
O professor titular da turma juntamente com o investigador, definiu objetivos, planeou e preparou as aulas de conteúdos no domínio geométrico a serem desenvolvidas num período de duas semanas e meia, como se explica no ponto seguinte. As tarefas planeadas foram resolvidas individualmente ou em par pedagógico, discutida a sua resolução e, no final, realizadas reflexões sobre as temáticas produzidas.
Recolheram-se todas as produções das crianças e as notas de campo que foram refletidas e alvo de análise do significado das respostas das crianças, bem como de toda a dinâmica comunicacional e procedimental desenvolvidas nas aulas aquando da exploração do GeoGebra.
Caraterização do contexto educativo e programático
A turma, enquanto objeto de investigação, é constituída por 11 raparigas e 12 rapazes. É uma turma heterogénea do ponto de vista do gosto manifestado pela Matemática e, em relação ao desempenho na disciplina, também revela alguma irregularidade. No seu percurso escolar ao longo do primeiro ciclo, o documento orientador das suas aprendizagens foi o PMEB (2007), alterando, no quinto ano, para o PMEB (2013).
No Programa de Matemática do ensino Básico (2007) apresentava-se no tema Geometria e Medida um tópico relacionado com as isometrias – “Reflexão” – com três objetivos específicos para os 1.º e 2.º anos: identificar no plano figuras simétricas em relação a um eixo; desenhar no plano figuras simétricas relativas a um eixo horizontal ou vertical e resolver problemas envolvendo a visualização e a compreensão de relações espaciais (p. 22) e outros três para o 3.º e 4.º anos de escolaridade: identificar no plano eixos de simetria de figuras; construir frisos e identificar simetrias; resolver problemas envolvendo a visualização e a compreensão de relações espaciais (p. 23). Nas notas para o professor acrescentava-se ainda que se deveriam explorar “frisos identificando simetrias, de translação, reflexão, reflexão deslizante e rotação (meia-volta)” (p.23), pelo que seria de supor que os estudantes tivessem algum conhecimento sobre o conteúdo – isometrias do plano. Assim, o trabalho desenvolvido obedeceu ao esquema seguinte:
1. Uma aula de 50 minutos na qual se procedeu a uma avaliação diagnóstica. Para tal aplicou-se um teste sobre isometrias e simetrias de reflexão e rotação;
2. Cinco aulas de 50 minutos nas quais se exploraram os conceitos de isometria, simetria, reflexão axial, reflexão central e rotação. No desenvolvimento destas aulas foi implementada a seguinte estratégia – (a) exploração, individualmente ou em pares, das tarefas; (b) partilha e discussão das resoluções dos estudantes, apoiadas pelo quadro branco, quadro com grelha quadriculada e GeoGebra;
3. Duas aulas de 50 minutos, nas quais os estudantes foram divididos em dois grupos, tendo-lhes sido proposta a resolução, individualmente, de uma tarefa. Numa das aulas, um dos grupos teve a possibilidade de utilizar o GeoGebra, e o outro grupo só pôde usar as ferramentas tradicionais. Na aula seguinte, o grupo que só usou as ferramentas tradicionais, pôde utilizar o GeoGebra e o outro grupo não. Com esta divisão procurou-se, por um lado, percecionar as dinâmicas de trabalho geradas com e sem o apoio do GeoGebra e, por outro, prestar um apoio mais individualizado aos estudantes, decorrente das dificuldades que fossem surgindo na utilização do programa.
5. Duas aulas para discussão e apresentação dos resultados das tarefas resolvidas.
6. Uma aula para resolução de uma ficha individual sobre os conteúdos explorados.
7. Uma aula para correção e partilha de resultados.
RESULTADOS E COMENTÁRIOS
Avaliação diagnóstica
No teste inicial os estudantes revelaram muitas dificuldades em resolver questões relacionadas com isometrias de reflexão e de rotação.
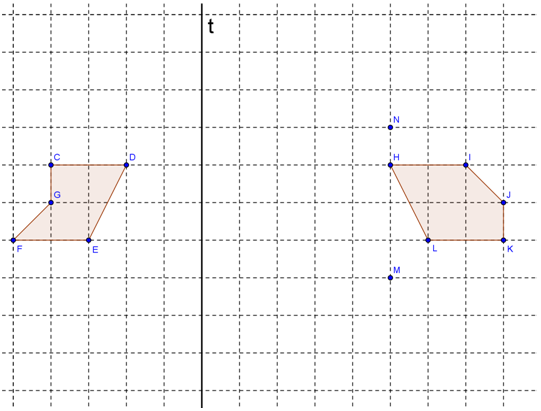
Figura 1. Tarefa de diagnóstico proposta aos alunos
|
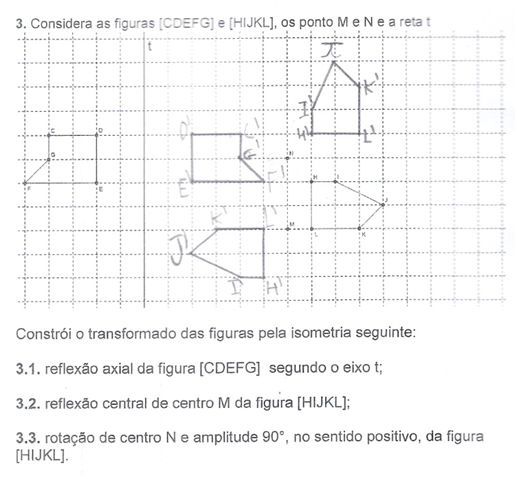
3. Considera as figuras [CDEFG] e [HIJKL], os ponto M e N e a reta t
Constrói o transformado das figuras pela isometria seguinte: 3.1. reflexão axial da figura [CDEFG] segundo o eixo t; 3.2. reflexão central de centro M da figura [HIJKL]; 3.3. rotação de centro N e amplitude 90°, no sentido positivo, da figura [HIJKL]. |
Na resolução da tarefa, nenhum aluno mostrou conhecimentos sobre reflexão central, nem foi capaz de construir a rotação e apenas cinco estudantes conseguiram fazer corretamente a isometria de reflexão axial.
Tendo em conta os resultados da avaliação diagnóstica, verificou-se que os estudantes não tinham grandes conhecimentos sobre os conteúdos.
Aulas/implementação de tarefas
Nas aulas destinadas à introdução dos conceitos, os estudantes, num primeiro momento, realizaram a pares, uma tarefa/questão sobre o conteúdo em estudo. Na realização da tarefa, os estudantes utilizaram os materiais tradicionais, papel, lápis, compasso, régua, esquadro e transferidor.
Num segundo momento procedeu-se à apresentação e discussão dos resultados obtidos, esclarecendo as dúvidas dos estudantes. Nestes momentos de partilha e de discussão de resultados, foram utilizados o quadro branco e quadriculado e o GeoGebra.
Numa destas aulas, explorando as isometrias de rotação, os estudantes construíram imagens de figuras geométricas planas por rotação utilizando régua e transferidor. Na apresentação e discussão de resultados, um grupo de estudantes fez a construção no quadro, explicando o processo aos restantes colegas.
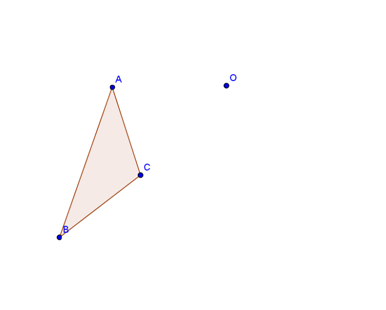
Figura 2. Exemplo de tarefa proposta aos alunos
|
Constrói a figura [A´B’C’], transformado do triângulo [ABC] por uma rotação de centro O e amplitude 70º no sentido negativo. |
Vejamos alguns dos diálogos desenvolvidos.
Aluno A – Começamos por desenhar retas entre o ponto A da figura e o centro de rotação. (traça o segmento de reta)
Aluno B – Depois fazemos o mesmo para os outros pontos. (começa a traçar os segmentos de reta)
Aluno C – Agora pegamos no compasso e fazemos circunferências por cima de cada ponto. (começa a traçar arcos)
Aluno A – Agora marcamos os ângulos. Colocamos o transferidor por cima linha e marcamos 70º.
Aluno D – Como é que fizeste?
Aluno A – Pões o transferidor por cima da reta OA, depois medes os 70º e marcas (o aluno volta a exemplificar). Aqui é o ponto A’
Aluno B – Agora pomos o transferidor no OB e marcamos outra vez 70º. É o B’.
Aluno C – Agora marcamos o ponto C’ (marca o ponto usando o transferidor)
Aluno A – Pegamos na régua e unimos os pontos A’, B’ e C’.
Posteriormente, a mesma construção foi realizada por um outro grupo de estudantes apoiado pelo professor, utilizando o GeoGebra, familiarizando os estudantes com o programa. No final da construção, foi feita a validação do trabalho dos estudantes, utilizando a ferramenta disponível no GeoGebra para a construção de rotações (dado o objeto, o centro e a amplitude). Depois, utilizando um seletor, procedeu-se à animação da rotação, fazendo variar a amplitude do ângulo. Este momento, proporcionado pelo dinamismo do programa, foi particularmente importante na compreensão do conceito de rotação.
Numa fase posterior, em duas aulas, foi proposta a resolução de duas tarefas idênticas às apresentadas na avaliação diagnóstica e nas condições de resolução referidas na metodologia.
Na resolução da tarefa seguinte, era pedido que identificassem imagens de figuras geométricas planas por reflexão central, reflexão axial e rotação:
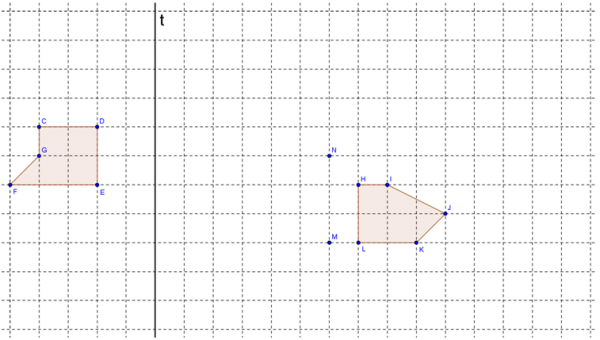
Figura 3. Exemplo de tarefa proposta aos alunos
|
Os polígonos seguintes são geometricamente iguais. |
2.1. Indica o polígono que corresponde ao transformado do polígono [CDEF]:
2.1.1. por uma rotação de 90º no sentido positivo;
2.1.2. por uma reflexão de eixo AB;
2.1.3. por uma reflexão central.
2.2. Indica o centro da rotação da alínea 2.1.1.
2.3. Indica o ponto da reflexão central da alínea 2.1.3.
Constatou-se que o grupo de estudantes que pôde recorrer ao GeoGebra se mostrou mais motivado na resolução da tarefa em comparação com o grupo que não teve acesso ao programa. Observou-se, ainda, que o facto de terem a possibilidade de utilizar uma ferramenta que lhes permitia validar as suas respostas, lhes possibilitou uma maior autonomia, estando menos dependentes do professor para avançar.
Na questão 2.2 e 2.3 observou-se que o dinamismo do GeoGebra ao possibilitar a movimentação dos pontos (centro de rotação e ponto de reflexão central) permitiu que os estudantes explorassem as suas ideias sobre qual o ponto que consideravam ser o centro de rotação e o ponto de reflexão central e corrigissem eventuais erros, isto porque depois de indicarem o ponto que consideravam ser a resposta certa, usavam o GeoGebra para confirmar.
Durante a resolução das tarefas, observou-se que o grupo que teve acesso ao programa, comparativamente com o outro grupo, conseguiu detetar os erros cometidos e corrigi-los.
Na resolução de outra tarefa, era-lhes proposto que construíssem imagens de figuras geométricas planas por reflexão central, reflexão axial e rotação utilizando régua, compasso e transferidor.
Figura 4. Exemplo de tarefa proposta aos alunos
|
3. Considera as figuras [CDEFG] e [HIJKL], os ponto M e N e a reta t |
Constrói o transformado das figuras pela isometria seguinte:
3.1. reflexão axial da figura [CDEFG] segundo o eixo t;
3.2. reflexão central de centro M da figura [HIJKL];
3.3. rotação de centro N e amplitude 90°, no sentido positivo, da figura [HIJKL].
Mais uma vez, o grupo que teve acesso ao GeoGebra conseguiu corrigir os erros cometidos, ou ultrapassar dúvidas que foram surgindo sem necessidade de intervenção do professor.
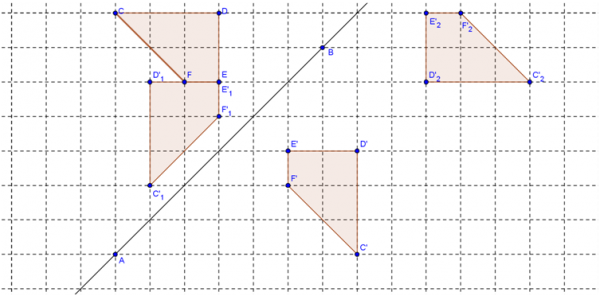
Figura 5. Resolução de um aluno
Este trabalho de complementaridade possibilitou uma melhor compreensão das isometrias do plano, permitindo que os estudantes desenvolvessem de uma forma mais sustentada a capacidade de identificar e construir imagens de figuras geométricas planas por reflexão central, reflexão axial e rotação.
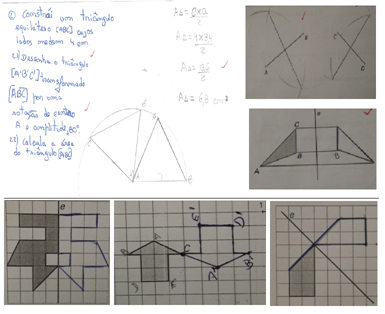
Alguns dos trabalhos dos estudantes, referindo-se ainda que nos transformados as crianças não se preocupam com o pormenor do preenchimento do elemento em causa.
Figura 6. Resoluções de alunos
No final, foi pedido aos estudantes que se pronunciassem sobre se o GeoGebra os tinha ajudado na resolução das tarefas. Todos os estudantes responderam que sim, considerando que os ajudaram a compreender melhor as reflexões e as rotações.
Figura 7. Opinião de um aluno sobre o GeoGebra
REFLEXÕES FINAIS
No trabalho desenvolvido não procuramos substituir o uso de ferramentas mais tradicionais, como a régua e o compasso, ou outros materiais manipuláveis, como as miras, pelas tecnologias informáticas, mas antes avaliar as potencialidades da complementaridade entre ambas. O estudo realizado permitiu-nos percecionar algumas vantagens desta complementaridade, com impacto positivo no conhecimento dos estudantes sobre os conteúdos em estudo. A utilização do GeoGebra permitiu, a par de uma maior motivação para a aprendizagem, que os estudantes construíssem, visualizassem, manipulassem e estabelecessem relações entre as propriedades dos objetos geométricos, de uma forma dinâmica. Este dinamismo e capacidade de visualização foi, segundo os próprios estudantes, particularmente importante na compreensão da isometria e simetria de rotação. Pode-se concluir que estes resultados vão na mesma linha de outros obtidos sobre esta problemática (Oliveira, 2012; Coelho, 2013; Gaspar & Cabrita, 2014).
Durante as aulas sobre este conteúdo, as ferramentas tecnológicas surgiram como complementares às ferramentas tradicionais, constituindo-se como um recurso importante na discussão entre os estudantes e o professor sobre o trabalho desenvolvido, nomeadamente pela possibilidade de visualizar no ecrã, de uma forma dinâmica, os efeitos das diversas transformações geométricas, contribuindo para o desenvolvimento da comunicação matemática. (Breda et al, 2011). Neste contexto educativo observou-se um diálogo mais consistente entre os estudantes, com o uso de um vocabulário adequado ao conteúdo. Pode-se, assim, concluir que o uso dos dois tipos de ferramentas proporcionou a aprendizagem e consolidação de termos próprios sobre isometrias. Nesta sequência, os diálogos estabelecidos entre os estudantes revelaram aprendizagens mais significativas e relacionais sobre o tema.