Fundamentación teórica
Esta investigación surge en el ámbito de la Teoría Antropológica de lo Didáctico (TAD), iniciada por el investigador francés Yves Chevallard en los años 80. En esta teoría se describe la estructura de una praxeología u organización matemática según cuatro componentes: tipos de tareas, técnicas, tecnología y teoría (Chevallard, 1999).
En 2005, fue introducida por Chevallard la noción de Recorrido de estudio e investigación (REI) que consiste en un dispositivo didáctico que prioriza el carácter funcional de las matemáticas al partir de la exploración de una cuestión Q con fuerte poder generador, en el sentido de ser capaz de propiciar la aparición de numerosas cuestiones derivadas. Para poder dar respuesta a dichas cuestiones, se requiere la reconstrucción de un número considerable de herramientas matemáticas (técnicas, nociones, propiedades, etc.), que aparecen así como una consecuencia (y no como el origen) del estudio de las cuestiones. La propuesta de los REI pretende recuperar la relación genuina entre cuestiones y respuestas que está en el origen de la construcción del conocimiento científico en general y de la actividad matemática en particular. Otro de los objetivos de la propuesta de los REI es el de introducir en la escuela la epistemología que se propone reemplazar el paradigma escolar monumentalista, que se caracteriza por el inventario y la exposición de los saberes, por un paradigma del cuestionamiento del mundo, para dar sentido al estudio escolar de las matemáticas en su conjunto, transportando a la escuela una actividad de estudio más cercana al ámbito de la investigación.
Así, se postula que la utilización de herramientas TIC podrá desempeñar un papel esencial en ese acercamiento en el sentido de fomentar la exploración y la capacidad de investigación, la formulación de conjeturas, la comparación del coste y amplitud de diferentes técnicas para resolver determinadas tareas y la validación de las respuestas a esas mismas tareas.
La TAD define la modelización matemática, y en particular la modelización funcional, como un proceso de reconstrucción y articulación de praxeologías matemáticas de complejidad y completitud crecientes. Este proceso parte de cuestiones problemáticas que una comunidad de estudio se plantea y que constituyen la «razón de ser» de las praxeologías matemáticas que es necesario (re)construir a modo de respuesta. La investigación explora los márgenes de libertad que ofrece para la experimentación de nuevas organizaciones didácticas que rompen con la enseñanza tradicional de las matemáticas y permiten analizar la potencialidad de los REI como dispositivos viables para una enseñanza funcional de las matemáticas entendidas como una herramienta de modelización (Serrano, 2013).
De modo análogo, en Barquero (2009) y Ruiz-Munzón (2010) se responde al fenómeno de la rigidez, desarticulación e incompletitud relativa de las organizaciones matemáticas escolares y, en particular, se intenta superar las dificultades con las que se encuentra la modelización matemática, con el diseño y experimentación de recorridos de estudio e investigación (REI) que se estructuran en secuencias de tareas bien articuladas que permiten el estudio progresivo de organizaciones matemáticas cada vez más amplias y completas.
Construcción de un recorrido de estudio e investigación
En esta sección se presenta una propuesta didáctica para levar a cabo con estudiantes del 11. º año de escolaridad de la enseñanza portuguesa (estudiantes con 16-17 años).
Para la construcción de la secuencia de tareas utilizamos ciertos indicadores de la calidad de la actividad matemática a desarrollar (en el sentido de Fonseca, (2004)) como, por ejemplo: la comparación del coste y de validez de diferentes técnicas, la inversión y interpretación de las técnicas, el desarrollo de actividades de modelización funcional que incluyan la utilización de herramientas informáticas que permitan la construcción de conocimiento o la modificación de las condiciones iniciales de un modelo para estudiar diversos sistemas matemáticos o extramatemáticos.
En este trabajo vamos a describir la potencialidad del software GeoGebra como una herramienta particular de las TIC en el proceso de enseñanza-aprendizaje. Así, además de ser un instrumento que permite articular los diferentes registros de una función (registro numérico, gráfico y algebraico), también es muy eficiente y dinámico tanto para hacer posible la visualización simultánea de los registros citados, como para explicitar la relación entre las modificaciones de los modelos funcionales y los cambios en sus parámetros.
En un primer contacto con el alumnado se pretende verificar los conocimientos previos adquiridos en relación al estudio algebraico de funciones polinómicas y sus representaciones gráficas, esencialmente de funciones afines, cuadráticas, cúbicas y cuárticas. Se espera que el alumnado reconozca determinadas características fundamentales de una función, tales como: el dominio y contra-dominio, el signo de una función, los ceros, la continuidad, la paridad, la monotonía y los extremos.
En esta etapa, el profesor puede inferir la legitimidad funcional del estudio del cálculo variacional al presentar una cuestión generatriz concreta como, por ejemplo:
Q:¿Cómo comparar la variación del número de infectados por una epidemia en los diversos instantes del tiempo?
Tarea 1:
|
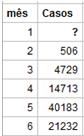
En 2009, las autoridades de salud pública de Brasil estaban muy preocupadas con la evolución de una epidemia de gripe H1N1. Conociendo los datos reales relativos al número de infectados entre los meses de mayo y de septiembre de 2009:
¿Cómo podrían prever lo que se pasaría en el mes de octubre? ¿Cuál sería el valor máximo de infectados? Estima el número de casos que ya existían al final del mes de abril. |
Para resolver este tipo de problema, el alumno va a sentir la necesidad de construir un modelo funcional. Podrá hacerlo analíticamente utilizando el hecho que para ajustar n puntos discretos dados existe siempre un polinomio interpolador de grado no superior a n-1 que pasa exactamente por esos puntos, o sea, que verifica determinadas condiciones.
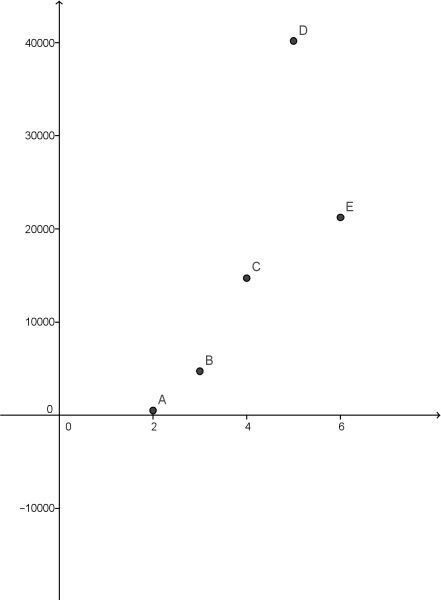
En este caso particular, el alumno deduciría un polinomio interpolador de grado 4 por el método de los coeficientes indeterminados, sabiendo que este pasa por los 5 puntos:
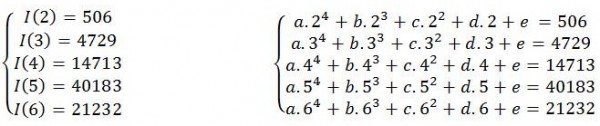
Dado el elevado coste de la técnica de resolución del sistema anterior, el estudiante va a sentir necesidad de buscar una técnica más económica. En este punto, el profesor podría conducir el alumnado a utilizar una técnica de exploración con el GeoGebra y, posteriormente, una técnica de validación:
Técnica 1: La manipulación de los parámetros para encontrar el modelo que mejor se ajusta a los puntos
Respuesta 1: Con esta técnica el estudiante podría estudiar la influencia que cada uno de los parámetros tiene en la forma de la gráfica de la función y concluir que, por ejemplo, el parámetro e es “responsable” del desplazamiento vertical de la gráfica y que corresponde a la ordenada en el origen. Sin embargo, en este caso, dados los elevados órdenes de magnitud va a resultar muy difícil descubrir los valores de los parámetros mediante su manipulación.
Técnica 2: La utilización directa de los comandos “polinomio” interpolador o regresiones polinómicas (estando subyacente la teoría de los mínimos cuadrados)
Respuesta 2: Aplicando una regresión polinómica a los datos discretos reales, obtenemos el siguiente modelo cuártico:
Modelo algebraico-funcional del número de infectados por la epidemia
![]()
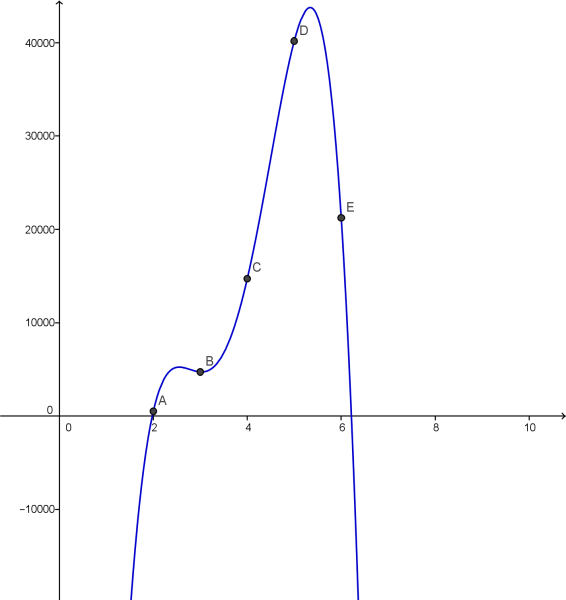
Figura 1 – Modelo gráfico-funcional del número de infectados por la epidemia
Al que al interpretar el modelo construido en el contexto del problema, vamos a considerar una restricción del dominio al intervalo [2; 6,22].
Así, podremos verificar que el GeoGebra podrá tener un papel primordial en el proceso de construcción de modelos funcionales a partir de datos discretos, sin embargo, es importante reseñar que el alumno deberá primero percibir los procedimientos algebraicos subyacentes a la simple ejecución de un comando automático. O sea, el alumno debe entender lo que el programa está haciendo y qué técnica algebraica está siendo automatizada.
Con el modelo ya construido, podremos plantear, por ejemplo, el siguiente tipo de tareas:
Tarea 2:
|
T2: Considerando el modelo cuartico anterior, T21: Determine los valores de las diferencias entre el número de infectados en dos meses consecutivos. ¿Cómo se podrá interpretar la última diferencia en el contexto real del problema? T22: ¿Cuál fue la variación media de infectados observada entre el segundo y el sexto mes? ¿Qué significa este valor? T23: ¿Cómo podremos descubrir la variación media que ocurrió entre dos meses cualesquiera? ¿Qué representa dicha variación media en términos geométricos? |
En una actividad exploratoria el alumnado podrá utilizar ciertas técnicas rudimentarias y sencillas, tales como:
Técnica 1: La determinación algebraica de la Tasa de Variación Media (con lápiz y papel)(*)
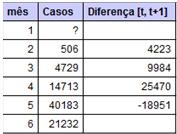
Tabla 1 – Cálculo de las diferencias entre el número de infectados por la epidemia en t+1 y en t.
En este punto, el profesor podrá conducir el estudiante a interpretar el signo de la última diferencia (I(6) – I(5)<0) :
El valor -18951 no significa que la función sea siempre decreciente entre el quinto y el sexto mes, sólo significa que el número de infectados ha sufrido un decrecimiento entre esos dos instantes, o sea, que I(6) < I(5).
En este momento el alumnado podrá conjeturar que para determinar la tasa de variación media, es necesario descubrir la diferencia entre el número de personas infectadas y repartir (dividir) por el total de intervalos unitarios comprehendidos. Por ejemplo, entre el segundo y el sexto mes, tenemos 4 intervalos unitarios, luego:
![]()
Lo que significa que entre el mes de mayo y el mes de septiembre, el número de individuos infectados aumentó, en media, cerca de 5182 personas por mes.
Mediante una actividad de institucionalización se podrá generalizar la situación tomando la tasa de variación media como una razón entre dos magnitudes y reseñar que, en el ámbito del estudio de la variación de modelos, ésta es una medida más fina que la diferencia de una cierta magnitud entre dos instantes consecutivos.
Exploración y trabajo de la técnica:
Para descubrir la variación media que ocurrió entre dos meses arbitrarios, el estudiante podrá, primeramente, experimentar calcular la tasa de variación media en diversos intervalos con lápiz y papel. Cuando ya dominar la técnica algebraica, el alumnado podrá:
I. Por un lado, intentar describir el modelo algebraico variacional asociado a la función Tasa de Variación Media en un intervalo genérico:
![]()
Simplificando, la expresión algebraica anterior obtendríamos:
![]()
Nótese que podrá ser una técnica muy costosa asociada a la manipulación de un modelo dependiente de dos parámetros a y b.
II. Por otro lado, verificar la existencia de la relación entre la TVM y la razón entre la diferencia de ordenadas de 2 puntos y las abscisas de eses mismos puntos, o sea:
![]()
Esta relación nos llevará a concluir que, en términos de la Geometría Analítica, la TVM en [a, b] representa la pendiente de la recta que pasa por los puntos del gráfico correspondientes a las abscisas a y b.
Cuestionamiento tecnológico
Dado que la determinación algebraica de la tasa de variación media con lápiz y papel es una técnica muy rudimental y que, dependiendo del modelo algebraico, puede tornarse un proceso extremamente costoso y poco fiable, se intentará encontrar una técnica mejor, más económica y fiable, esto es, que reduzca la probabilidad de cometer errores de cálculo.
Para que la actividad matemática sea más completa es importante estudiar diferentes técnicas para resolver un determinado tipo de tareas y explicitar los criterios que permiten elegir la técnica más adecuada en cada caso. Así, podremos verificar la interpretación geométrica de la TVM en [a, b] con el GeoGebra, partiendo de una adaptación y ampliación de una técnica de Mario Sánchez Aguilar (2006):
Técnica 2: Determinación algebraica y gráfica de la TVM con el GeoGebra
Descripción detallada de la técnica:
-
Representar gráficamente la función y 2 puntos aleatorios A y B de su gráfico;
-
Mover el punto A y registrar su trazo, después a medida que se mueve el punto B, registrar el trazo del punto B en una hoja de cálculo.
-
A partir de las coordenadas de los puntos A y B y usando las células correspondientes en la hoja de cálculo, podremos definir la TVM en el intervalo [a, b], obteniendo los siguientes valores de la TVM:
Figura 2 – Interpretación gráfica de una TVM negativa de infectados con el GeoGebra
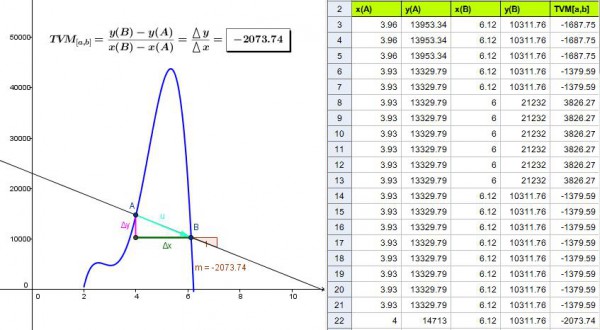
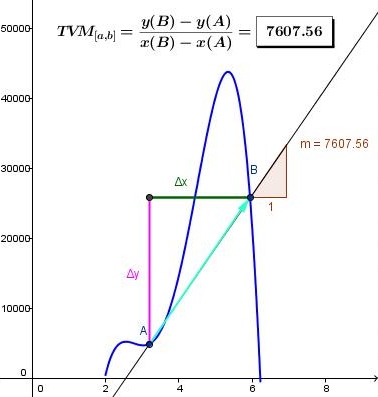
Figura 3 – Interpretación gráfica de una TVM positiva de infectados con el GeoGebra
Al utilizar esta técnica el alumnado podrá verificar el siguiente:
Para cualesquier puntos A y B, el valor de la TVM coincide siempre con la pendiente de la recta AB (designada por m y representada gráficamente por la razón entre las magnitudes correspondientes a la variación de las ordenadas y a la variación de las abscisas de los respectivos puntos, o sea, Δy/Δx).
Comparación de dos técnicas
Una gran ventaja de la técnica 2 (con GeoGebra) sobre la técnica 1 (con lápiz y papel), además de permitir la determinación inmediata de la TVM para cualquier intervalo recurriendo a un proceso algorítmico eficiente y rápido, reside en la posibilidad de adaptar y reproducir la técnica construida (ya programada) para resolver tareas asociadas a otras situaciones problemáticas. Este procedimiento es viable porque el GeoGebra permite visualizar los efectos de la manipulación y los cambios provocados por la modificación de las condiciones iniciales del problema. Así, el profesor podrá explorar distintos casos que pueden ser interesantes en el proceso de enseñanza-aprendizaje de una determinada praxeología matemática.
Por ejemplo, podría aprovechar la posibilidad de mover el punto B muy cerca del punto A para construir el concepto de derivada de una función:
Actividad exploratoria
El profesor podría conducir el estudiante a testar el siguiente:
A fin de comparar los valores de los infectados a lo largo del tiempo, podremos ampliar la técnica anterior fijando ahora el punto A y, registrando (en la hoja de cálculo) solo el trazo del punto B a la medida que este se mueve acercándose al punto A, como sigue:
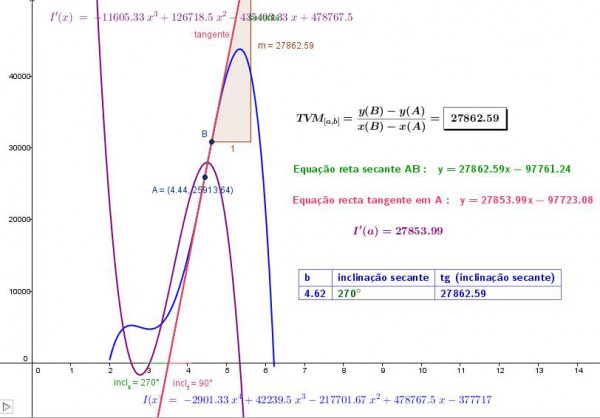
Figura 4 – Interpretación de la “TVM en un punto” con el GeoGebra
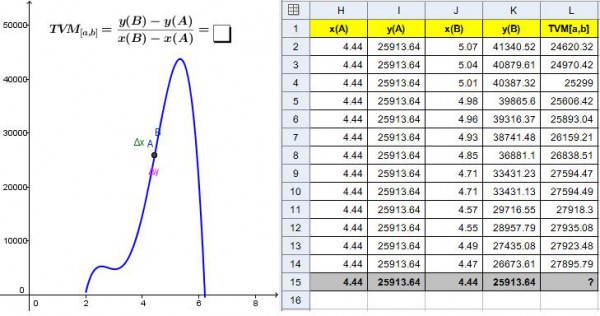
Podremos observar que, a la medida que el punto B se va a aproximar del punto A y la amplitud del intervalo [a, b] se reduce, los valores de la TVM en [a, b] se aproximan a 27872 infectados.
Además, los estudiantes pueden observar que cuando el punto B está muy próximo al punto A, más aún, cuando sus coordenadas coinciden, entonces el valor de la TVM en el intervalo [a, b] no se puede determinar, como muestra la última línea de la tabla.
De hecho, cuando el punto B coincide con el punto A, entonces la TVM ya no representa un valor medio, sino un valor instantáneo designado por la Tasa de Variación Instantánea de los infectados 4,44 meses después de la propagación de la epidemia.
Así, podremos decir que, en cuanto que la tasa de variación media se calcula entre 2 valores del tiempo, la tasa de variación instantánea se determina en 1 sólo instante.
|
¿Cómo vamos conseguir calcular el valor de la Tasa de Variación Instantánea de los infectados 4,44 meses después de la propagación de la epidemia? |
Trabajo de la Técnica
Técnica 2.1: La determinación algebraica de la Tasa de Variación Instantánea (con lápiz y papel)
Retomando el modelo algebraico variacional asociado a la función Tasa de Variación Media en un intervalo genérico [a, b], el profesor podrá particularizar y describir el modelo algebraico variacional de los infectados por la epidemia en el intervalo [4,44; b]:

Simplificando, obtenemos el siguiente modelo variacional:
![]()
Nótese que el modelo algebraico variacional asociado a un modelo algebraico funcional cuártico es un modelo cúbico.
Haciendo el instante de tiempo b coincidir con el instante de tiempo a, resulta:

Lo que significa que, cuando el punto B coincide con el punto A, entonces la Tasa de Variación Instantánea de los infectados 4,44 meses después de la propagación de la epidemia es, aproximadamente, de 27639 infectados por cada mes.
Interpretación y ampliación de las técnicas
Recurriendo a una técnica más completa que permite relacionar el estudio de diferentes praxeologías matemáticas:
Técnica 3: La determinación geométrica de la Tasa de Variación Instantánea y su relación con la Tasa de Variación Media (con el GeoGebra)
Descripción detallada de la técnica:
-
Representar gráficamente la función y 2 puntos aleatorios A y B de su gráfico;
-
Introducir la expresión de la Tasa Media de Variación en la entrada de comandos del GeoGebra a partir de eses 2 puntos;
-
Crear la recta secante AB y verificar que su pendiente coincide con el valor de la TVM;
-
Crear la recta tangente al gráfico de la función en el punto A;
-
Establecer la relación entre la pendiente de la secante y la tangente de su inclinación;
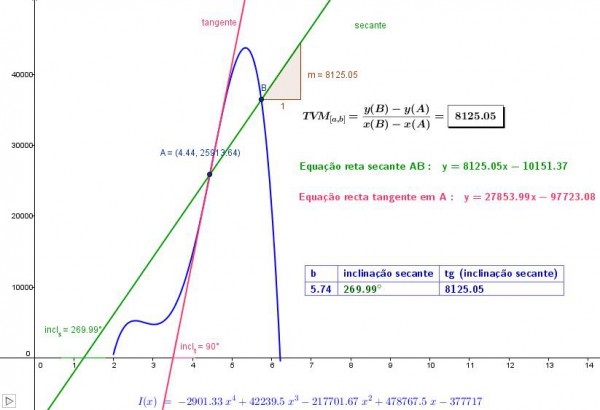
Figura 5 – Relación entre la tasa de variación instantánea y la tasa de variación media (en GeoGebra)
Una de las principales ventajas de esta técnica es que, sí el alumno manipula el punto B y lo va acercando al punto A, podrá observar que la recta secante AB tiende a la recta tangente al gráfico en el punto A. Lo que implicará que sus pendientes se tornen muy próximas, o sea, que el valor de la TVM – Tasa de Variación Media (pendiente de la recta secante AB) sea muy próximo del valor de la TVI – Tasa de Variación Instantánea (pendiente de la recta tangente al gráfico en A).
Institucionalización
Concluimos así que, cuando B se aproxima de A:
![]()
Habitualmente se designa la Tasa de Variación o Tasa de Variación Instantánea en el instante a = x(A) por la derivada en ese mismo instante que, en este caso particular, representamos por I’(a) o por
![]()
También podremos observar que, cuando B se aproxima de A, la sucesión de las tangentes de las inclinaciones de las rectas secantes se aproxima del valor de la derivada de la función en el punto A, o sea:
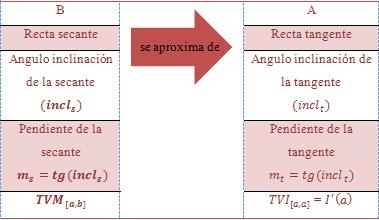
Tabla 2 – Consecuencias de la aproximación del punto B al punto A
El profesor podría conducir las siguientes cuestiones:
Identifique en el gráfico, un punto en lo cual la TVI es aproximadamente igual a cero. ¿Qué significa la anulación de la TVI? ¿Qué sucede en un intervalo de ese punto? ¿Qué representará ese punto?
Sí la TVI es igual a cero, entonces la recta tangente al gráfico del modelo presenta una pendiente igual a cero, o sea, es una recta horizontal paralela al eje de los xx.
Sí en un entorno de ese punto hay un cambio en el signo de la TVI y, consecuentemente, un cambio en el sentido de crecimiento/decrecimiento del número de infectados entonces, ese punto representa un extremo relativo del gráfico de la función. En este caso particular, representa el valor máximo de infectados por la epidemia.
Y el alumno podría cuestionarse:
¿Esto significa que siempre que se pretenda calcular la derivada de la función en un determinado instante se tendrán que calcular varias TVM para aproximar así el valor de la TVI o derivada en ese punto? ¿Se tendrá que aplicar esta técnica una infinidad de veces? ¿No existe una técnica más rápida y menos costosa?
Nótese que a cada instante del tiempo corresponde un único valor de infectados y, por tanto, un único punto del gráfico y consecuentemente, una única recta tangente, que a su vez, tiene una única pendiente. Así, a cada instante del tiempo corresponde un único valor de derivada, lo que significa que la relación entre la derivada de la función y el tiempo es una relación funcional. Por tanto, podremos hablar de la función derivada.
Partiendo de datos discretos relativos a valores de la TVI/derivada en algunos instantes presentados en una tabla, podremos represéntalos gráficamente y con el GeoGebra descubrir la expresión algebraica de la función derivada (modelo algebraico-diferencial).
Por otro lado, si construimos el trazo de las Tasas de Variación Instantáneas para los sucesivos instantes, obtenemos el trazado del gráfico de la función derivada de la función que representa el número de infectados en cada instante de tiempo.
A fin de confirmar que el valor de la función derivada de una función en un punto es igual a la pendiente de la recta tangente a la función en ese punto, el estudiante puede descubrir (con el auxilio del GeoGebra) gráficamente y algebraicamente la función derivada y calcular la derivada de la función en el punto A: I’(a) . Así, podremos:
-
Representar gráficamente y algebraicamente la función derivada de la función;
-
Calcular la derivada de la función en el punto A;
-
Aproximar el punto B del punto A.
Comparando el modelo algebraico diferencial representado en la figura por I’(x) con el modelo algebraico funcional I(x) podremos observar que la función derivada de un modelo cuartico será un modelo cúbico, como ya había pasado con el modelo algebraico variacional.
Conclusiones y futuras investigaciones
En el proceso de construcción de la propuesta didáctica descrita en la sección anterior, y según un análisis a priori de este recorrido de estudio e investigación, se destaca la versatilidad inducida en un proceso de enseñanza-aprendizaje por la utilización de determinadas herramientas del GeoGebra.
Más concretamente, el GeoGebra revela ser un instrumento informático con un papel primordial en la construcción de dispositivos didácticos para la enseñanza por permitir una visualización más amplia del problema, la manipulación de los datos y, consecuentemente, la exploración de otros problemas emergentes de forma autónoma por parte de los estudiantes. Así, estamos de acuerdo con el estudio efectuado por Ruiz, Ávila y Villa-Ochoa (2013), en lo cual se reseña que las actividades de aula, diseñadas específicamente para la producción del conocimiento a partir de la manipulación, la visualización, la utilización de software educativo y el uso de diversos contextos o representaciones, permiten que los docentes mejoren significativamente sus herramientas de trabajo dentro del aula y de esa manera los estudiantes tengan momentos de“diversión” y “tensión” que los llevan directamente a la búsqueda de diversos resultados generando en ellos un mayor sentido de competitividad (Ruiz, Ávila & Villa-Ochoa, 2013).
Por otro lado, el GeoGebra también funciona como herramienta de validación de las técnicas que utilizan solamente el lápiz y el papel, ya sean algebraicas, gráficas, aritméticas o numéricas. Sin embargo, reseñamos que la utilización de este instrumento informático no deberá emplearse de forma aislada, deberá ser siempre complementada con la fundamentación teórica que justifique una determinada técnica automática.
En el mismo sentido de esta aportación, ya en 2011, Michèle Artigue había notado las dificultades de determinados profesores (participantes de una investigación) en poner en marcha de manera razonada y eficaz la integración tecnológica deseada por una dada institución. En particular, había observado que: las técnicas instrumentadas dentro de ciertas clases experimentales eran legítimas pero no trabajadas oficialmente; dichas técnicas no hacían parte de los procesos de entrenamiento y de mecanización, como lo hacían las técnicas en lápiz y papel; no eran objeto de una institucionalización; el discurso tecnológico (en el sentido de la TAD) que las enmarcaba era limitado y esencialmente descriptivo, o sea, las técnicas se quedaban en un estado artesanal y no llegaban a adquirir, convenientemente seleccionadas y trabajadas, un estatus de técnicas expertas (Artigue, 2011). Como respuesta a este problema ha considerado necesario ayudar los profesores a: organizar una génesis instrumental institucional que sustentaría las génesis individuales esperadas, a organizar el trabajo de selección y de mejoramiento de las técnicas instrumentadas, a desarrollar un discurso tecnológico combinando saberes matemáticos y saberes artefactuales que no existía en ninguna parte para sustentar su institucionalización, a organizar la evolución de la relación de estas técnicas a lo largo del avance de los conocimientos al interior de la clase. Artigue ha reseñado que en las clases experimentales concernidas los efectos del trabajo descrito fueron evidentes.
De modo análogo se pretende, en futuras investigaciones, evidenciar empíricamente nuestras conclusiones al experimentar la propuesta didáctica desarrollada en este trabajo con profesores y estudiantes de la enseñanza secundaria portuguesa y, en un análisis a posteriori, evaluarla en términos de aportaciones para la didáctica de las matemáticas.
Agradecimientos
Este trabajo fue financiado por la beca SFRH/BD/77335/2011 de la FCT (Portugal) y por el proyecto “La modelización matemática para la formación del profesorado de secundaria: del algebra al cálculo diferencial” (EDU2012-39312-C03-03).