No Programa de Estudos Pós-Graduados em Educação Matemática da Pontifícia Universidade Católica de São Paulo – PUC/SP, a linha de investigação Tecnologias da Informação e Educação Matemática é objeto de pesquisa do grupo Tecnologias e Meios de Expressão em Matemática – TecMEM. As pesquisas desse grupo visam compreender as dificuldades existentes na prática de docentes de Matemática no uso das tecnologias, em especial das tecnologias digitais. Tais dificuldades dizem respeito à transposição didática dos saberes a ensinar e às possibilidades oferecidas pelas tecnologias para criar estratégias didáticas que permitam aprimorar e dinamizar o processo de construção do conhecimento matemático por parte de professores e lunos.

De acordo com Abar (2011):

(…) na era digital, não incorporar as tecnologias no processo educacional, é condenar à marginalidade todas as pessoas que não tenham a competência para utilizar os instrumentos tecnológicos que lhe possibilita o vínculo com a sociedade.

Importante observar que apenas a existência das tecnologias que permitem o rápido acesso às informações e à comunicação não garante a construção do conhecimento e de uma sociedade preparada para seu uso. Isso depende das pessoas e não das tecnologias utilizadas. Neste aspecto é que se sobressai o papel das tecnologias na educação: que seu uso seja direcionado à construção do conhecimento e à formação de pessoas competentes para a inserção em uma sociedade cada vez mais tecnológica. Deste modo o uso das tecnologias na educação não é um fim em si mesmo e sim um instrumento para o desenvolvimento cognitivo.

Também é essencial ter o entendimento de que se as tecnologias forem utilizadas simplesmente para transmitir informações, já elaboradas, no processo de aprendizagem, elas estarão a serviço de uma função pedagógica tradicional sem possibilitar nenhuma inovação ou mudanças por parte dos sujeitos envolvidos.

Assim, não basta incorporar as tecnologias no desenvolvimento profissional dos professores para que conheçam ou manipulem equipamentos tecnológicos. Essa incorporação deve estar presente em sua formação inicial e permanente, condição indispensável para que este futuro professor desenvolva a capacidade de buscar, usar e gerar informações, a qual só é possível com o apoio das tecnologias. Cada nova tecnologia que surge precisa ser aprendida, por meio de iniciativa própria ou por meio de cursos e a ajuda dos mais experientes.

É preciso buscar informações, realizar cursos, pedir ajuda aos mais experientes, enfim, utilizar os mais diferentes meios para aprender a se relacionar com a inovação e ir além, começar a criar novas formas de uso e, daí, gerar outras utilizações. Essas novas aprendizagens, quando colocadas em prática, reorientam todos os nossos processos de descobertas, relações, valores e comportamentos. (Kenski, 2007, p.44)

Estudos sobre práticas pedagógicas inovadoras e mediadoras de aprendizagens com o uso de tecnologias, procurando atender à diversidade e aos desafios contemporâneos da educação brasileira, têm sido realizados com sucesso pelos participantes do grupo TecMEM. Muitas destas pesquisas foram desenvolvidas com o uso do GeoGebra[1], que tem se revelado um importante recurso para contribuir com o ensino e aprendizagem da Matemática.

Podemos entender melhor a relevância do uso do GeoGebra por meio da análise das oportunidades pedagógicas, em níveis de: agilidade e precisão de tarefas; envolvimento sócio-afetivo com o conhecimento matemático; produtividade do ensino em sala de aula; desenvolvimento cognitivo e o domínio de habilidades tecnológicas integrado ao conhecimento matemático.

Pelo fato do GeoGebra possuir tantas oportunidades de exploração da Matemática nos diversos anos da vida escolar, além de seu livre acesso, é que podemos compreender sua rápida expansão com a criação de Institutos por todo o mundo. No entanto, há muito trabalho para que o GeoGebra e a Educação Matemática caminhem lado a lado para o aprimoramento do ensino e aprendizagem da Matemática.

Procurando colaborar com este cenário é que apresentamos, no IV Dia de GeoGebra de Portugal, as atividades que desenvolvemos em nossa Universidade, indicando sites na internet nos quais alguns trabalhos que utilizaram o GeoGebra podem ser acessados livremente.

Em 2011, quando realizamos, em São Paulo, a 1ª. Conferência Latino-americana de GeoGebra havia apenas três institutos na América Latina e hoje, em 2014, já são quase vinte. Os trabalhos apresentados nesse evento estão disponíveis na Internet conforme mostra a Figura1 a seguir, no volume 1, número 1 da Revista do Instituto GeoGebra de São Paulo, no endereço: http://revistas.pucsp.br/IGISP

Figura 1 – Revista do Instituto GeoGebra de São Paulo.

As informações sobre o Instituto GeoGebra de São Paulo, com sede na Faculdade de Ciências Exatas e Tecnologias da PUC/SP, também estão disponíveis endereço http://www.pucsp.br/geogebrasp, como indica a Figura 2 a seguir. Outras informações relevantes podem ser obtidas no site em questão.

Figura 2 – Página do Instituto GeoGebra de São Paulo.

Na aba Pesquisas e Publicações podem ser acessadas as dissertações de mestrado e teses de doutorado, de 2009 a 2011, cujas pesquisas utilizaram o GeoGebra, como pode ser verificado na Figura 3 a seguir.

Figura 3 – Página das Pesquisas e Publicações Instituto GeoGebra de São Paulo.

Outra atividade do grupo TecMEM é direcionada para a formação de professores para o uso do GeoGebra. De 2009 a 2011 foi oferecido, na PUC-SP, por meio da plataforma Moodle, um curso de extensão chamado “Matemática Dinâmica”, com 32 horas de atividades a distância e dois encontros presenciais de 8 horas. O curso era composto de módulos com conteúdos de Matemática que atendiam o currículo da escola básica. A Figura 4 apresenta a tela do curso em questão.

Figura 4 – Página do Curso Matemática Dinâmica a Distância.

Oficinas com pequenas turmas de, no máximo, 20 professores são oferecidas na própria Faculdade, aos sábados, para os interessados que se inscreveram por email. Em 2012 tivemos cinco turmas e em 2013, quatro turmas.

Atualmente oferecemos oficinas de GeoGebra pelo Skype durante 1 hora em cada conexão e em média cinco conexões. Esta proposta tem se mostrado bastante interessante e é utilizada a ferramenta de compartilhamento de tela do Skype. Normalmente são trabalhados os passos iniciais no uso do software, pois alguns participantes não conhecem o GeoGebra.

As atividades foram adaptadas do GeoGebra Workshop Handout, criado por Markus e Judith Hohenwarter. Na Figura 5 podemos observar a primeira página das atividades, em formato .pdf que são enviadas aos participantes por email.

Figura 5 – Página inicial da apostila das Oficinas de GeoGebra.

Nas disciplinas oferecidas aos alunos de mestrado e doutorado do programa de Pós-Graduação em Educação Matemática, a utilização do GeoGebra está presente em diversos tópicos da Matemática. Em uma das disciplinas, denominada Tópicos de Matemática Básica, são explorados conteúdos de Espaço e Forma, Grandezas e Medidas, Números e Operações, Equações, Inequações e Tratamento da informação (Estatística e Probabilidade). Em todos eles, a utilização do GeoGebra indica as potencialidades desse software.

A investigação matemática das dissertações e teses de alguns alunos do Programa de Estudos Pós-Graduados em Educação Matemática utilizam o GeoGebra em suas pesquisas. Assim, há vários trabalhos com propostas de atividades disponíveis na Internet com diversos aportes teóricos e diferentes metodologias. Os trabalhos podem ser acessados no endereço http://www.sapientia.pucsp.br/tde_busca/resultado-tdes-prog.php?ver=13&programa=13&ano_inicio=&mes_inicio=&mes_fim=&ano_fim=2013&grau=Todos

ou http://www.sapientia.pucsp.br/tde_busca/index.php?tipoPesquisa=1

Sugerimos, a seguir, duas dissertações de mestrado e uma tese de doutorado que fizeram uso do GeoGebra nas respectivas pesquisas. É possível usufruir das atividades já construídas e analisadas, sendo uma opção didática para a prática em sala de aula.

• Sergio Vicente Alencar: A gênese instrumental na interação com o GeoGebra: proposta de uma oficina para professores de matemática  e http://www.pucsp.br/tecmem/sergio_alencar.pdf
• Nilza Aparecida de Freitas: Sistemas de equações lineares: uma proposta de atividades com abordagem de diferentes registros de representação semiótica
• André Lúcio Grande: Um estudo epistemológico do Teorema Fundamental do Cálculo voltado ao seu ensino e http://www.pucsp.br/tecmem/Andre/GeoGebra-Andre/inicio.html

Com relação às Geometrias Não Euclidianas temos em nosso programa algumas pesquisas feitas, mas nenhuma utilizou GeoGebra. Uma delas, de 2004, de Eliane Cabariti, sobre Geometria Hiperbólica utilizou o Cabri: Geometria Hiperbólica: uma proposta didática em ambiente informatizado e outra de 2006, de João Pedro Marqueze, sobre Geometria Esférica: As faces dos sólidos platônicos na superfície esférica: uma proposta para o ensino-aprendizagem de noções básicas de Geometria Esférica, na qual utilizou material concreto. Ambas podem servir de referência para propostas de atividades sobre Geometrias Não Euclidianas.

Outros programas de Pós-Graduação de nosso país apresentam trabalhos sobre Geometrias Não Euclidianas com o GeoGebra, por exemplo, Maria Alice Gravina e Ricardo Silva Ribeiro em http://www.mat.ufrgs.br/~ppgem/produto_didatico/rribeiro/ disponibilizam o trabalho desenvolvido por eles.

Para contribuir um pouco mais com o tema, neste IV Dia de GeoGebra, apresentamos um modelo/plano de Geometria Não Euclidiana, a Elíptica, que pode ser acessado em http://www.pucsp.br/tecmem/OAs/reta_eliptica.html, no site do grupo TecMEM. Esse modelo foi construído no GeoGebra por meio de macros. A Figura 6 mostra a imagem inicial do modelo no qual várias atividades podem ser exploradas com a utilização das demais ferramentas do GeoGebra.

Um modelo em Geometria Plana Elíptica (devido a Klein) lembra o modelo de Poincaré para Geometria Hiperbólica. Neste modelo o plano é um círculo unitário (só que aqui estão incluídos os pontos da circunferência), os “pontos” são os pontos euclidianos dentro do círculo unitário, bem como os pares de pontos antípodas no círculo que são identificados. As “retas” são ou diâmetros do círculo unitário ou arcos das circunferências euclidianas que interceptam a circunferência do círculo unitário nas extremidades de um diâmetro

Figura 6 – Modelo para desenvolvimento de atividades sobre Geometria Elíptica.

Com esta atividade espera-se que haja o entendimento de uma nova ideia de reta

e se observe que, assim como na Geometria Euclidiana, por um ponto passam infinitas retas; que diferente da GE, duas retas sempre se interceptam e que por dois pontos podem passar infinitas retas. O segmento unindo os pontos A e B é o menor arco da reta determinada pelos pontos A e B, quando A e B não são antípodas. Se A e B são antípodas tem-se dois segmentos com extremidades em A e B.

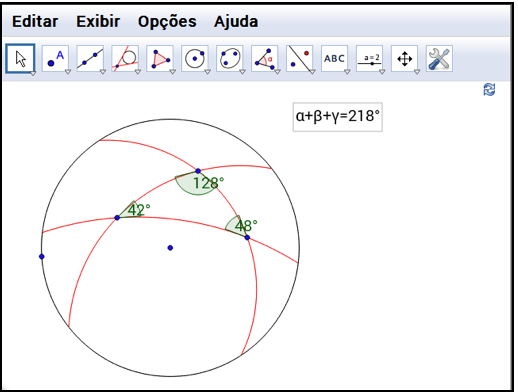
Para exemplificar a utilização do modelo, apresentamos a Figura 7 abaixo. Trata-se de uma atividade proposta para investigar qual é a soma das medidas dos ângulos internos de um triângulo elíptico. O resultado mostra que essa soma é maior que 180°, evidenciando uma propriedade dos triângulos elípticos.

Figura 7 – Atividade desenvolvida no modelo de Geometria Elíptica (fig7_abar_2014).

As atividades do grupo TecMEM desenvolvidas, e aqui expostas, são propostas que permitem a investigação e exploração destas geometrias pelos interessados, inseridas no tema do evento IV Dia de GeoGebra: para além de Euclides.

De modo geral, os resultados das pesquisas realizadas permitiram reconsiderar algumas escolhas, de acordo com a metodologia adotada, levando-nos à reelaboração de algumas propostas, em particular no que se refere à constituição e utilização das ferramentas disponibilizadas no GeoGebra. Alguns participantes observaram que o desconhecimento das possibilidades do GeoGebra e de sua utilização podem interferir no alcance dos objetivos propostos e, também, que é necessário um tempo mais adequado para a apropriação de suas possibilidades.

Este é um panorama geral do que nós temos feito para o Ensino e a para a Matemática com a utilização do GeoGebra.