1. Contexto da prática profissional
Atualmente, em Portugal, na disciplina de Matemática no 2.º ciclo do ensino básico são lecionadas as potências de base racional positiva e expoente natural, sendo outros expoentes mais gerais introduzidos no 3.º ciclo e no Ensino Secundário. A abordagem destes conteúdos pretende oferecer aos alunos um primeiro contacto com os métodos simbólicos próprios da Álgebra, que permitem deduzir e organizar um certo número de conhecimentos de forma sistemática (MEC, 2013).
Diversos estudos mostram que os alunos têm dificuldades em dominar e aplicar as regras das operações com potências (Birenbaum & Tatsuoka, 1993; Lay, 2006; Paias, 2009; Tseng, 2012) e apontam algumas estratégias para melhorar o ensino e a aprendizagem das mesmas.
A pesquisa levada a cabo por Birenbaum e Tatsuoka (1993) mostra o nível de desempenho dos alunos em relação às diferentes regras das operações com potências. Os autores administraram um teste de 38 itens a 431 alunos e os tópicos testados foram 12 envolvendo “definições e regras básicas, e os pré-requisitos necessários » (p. 259). Os 12 tópicos são apresentados na Figura 1.

Figura1- Tópicos do estudo de Birenbaum e Tatsuoka (1993, p. 259).
Birenbaum e Tatsuoka (1993) constataram que os alunos dominaram com mais facilidade as regras das potências que constam dos tópicos 2, 3 e 4 na Figura 1. As regras mais difíceis foram as que se listam da Figura 1, nos tópicos 5 e 6.
A investigação conduzida por Lay (2006) aponta estratégias úteis para o ensino e a aprendizagem das potências. Este autor defende que o estudo da definição de potência é mais eficaz no ensino e na aprendizagem das potências do que o estudo das regras dos expoentes para potências com a mesma base.
A potência representa um produto de fatores iguais. O fator é a base e o expoente é o número que define quantas vezes a base será multiplicada por ela mesma. Para o aluno entender o significado disto, o professor recorre a exemplos e escreve 2³=2×2×2,referindo que se trata de uma potência de base 2 e expoente 3.
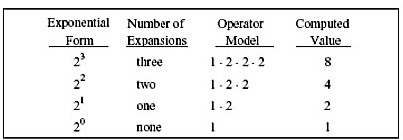
Há inúmeras maneiras que o professor pode utilizar no ensino do cálculo de uma potência, mas Lay (2006) afirma que o « melhor processo é utilizar a definição de potência fazendo o produto do número 1 (identidade da multiplicação) pelo número que se repete como fator. O expoente é o número de vezes que esse fator ocorre” (p. 131). Este método é ilustrado na Figura 2, no caso em que a base da potência é 2.
Figura2- Potências de base 2 (Lay, 2006, p. 131).
Segundo este autor, a ideia de potência de expoente natural deve ser entendida como o resultado da multiplicação de um dado número por si mesmo um certo número de vezes por 1. Ao número que se multiplica por si mesmo dá-se o nome de base da potência e ao número que nos indica o número de vezes que a base se multiplica por si mesma chamamos expoente. Embora o número 1 possa ser excluído da multiplicação, este deve ser conservado, porque ajuda os alunos a lembrarem-se que numa potência de expoente nulo e base não nula é sempre igual a 1 e não a zero.
Birenbaum e Tatsuoka (1993) descobriram que um dos itens mais difíceis para os alunos é o que se refere às potências de expoente zero. A estratégia apresentada por Lay (2006) pode ser ensinada em sala de aula para corrigir o erro de muitos alunos que atribuem o resultado zero, à potência de expoente nulo.
Paias (2009) realizou um estudo sobre o erro e a sua importância no ensino e aprendizagem, no âmbito das operações com potências, com 30 alunos da 8.ª série do ensino fundamental e 30 alunos do 1.º ano do ensino médio de uma escola estadual de São Paulo. Tratou-se de uma pesquisa com a realização de um teste diagnóstico sobre os erros dos alunos referentes às potências e às operações com potências. Os erros observados por Paias (2009) foram divididos nas seguintes categorias: erros relacionados com a técnica da definição; erros relacionados com a técnica da regra de sinais; erros relacionados com convenções matemáticas; erros relacionados com a presença de expoentes negativos; erros relacionados com propriedades de potenciação; erros relacionados com as bases fracionárias e erros relacionados com a operação multiplicação.
De acordo com Tseng (2012) é importante que o conhecimento dos alunos seja conceitual e não apenas processual quando se trata de compreender as regras operatórias das potências. O conhecimento conceitual é necessário para que os alunos percebam as regras das potências e não as memorizem. Tseng (2012) afirma que, para que os alunos obtenham o conhecimento conceitual, é necessário exemplificar a regra, antes de esta ser generalizada: “Por exemplo, na regra da multiplicação de potências com a mesma base e expoentes diferentes, os alunos têm necessidade de visualizar um exemplo do tipo (x¹)(x²)=x³. Isto significa que xxx=x³. Deste modo, os alunos vão perceber que na multiplicação de potências com a mesma base, adicionam-se os expoentes e obtém-se o expoente 3 e não se multiplicam 1×2=2” (p. 7).
No Programa e Metas Curriculares de Matemática do ensino básico (MEC, 2013), podemos constatar que no 7.º ano de escolaridade, no decurso do conteúdo das expressões algébricas, faz-se a extensão da definição e das propriedades das potências de expoente natural aos números racionais negativos No 8.º ano de escolaridade do ensino básico, está presente o tema das potências de expoente inteiro, lecionando-se pela primeira vez as potências de expoente nulo e as potências de expoente negativo e procede-se à extensão das propriedades conhecidas das potências de expoente natural às potências de expoente inteiro.
Documentos de orientação curricular e de investigação reconhecem que a aprendizagem dos alunos pode beneficiar muito da tecnologia, através da visualização de noções matemáticas sob múltiplas perspetivas e representações interligadas (NCTM, 2007; Ferrara, Pratt & Robutti, 2006).
O Programa de Matemática (MEC, 2013) incentiva o uso das tecnologias, embora recomende que estas sejam usadas com responsabilidade de modo a enriquecer e melhorar as oportunidades de aprendizagens matemáticas dos alunos. Os alunos são levados a trabalhar em níveis mais elevados de generalização ou abstração, uma vez que com o uso das tecnologias o aluno pode analisar mais exemplos ou visualizar diferentes formas de representação, conduzindo-o a formular conjeturas, que manualmente, seriam demorados, (NCTM, 2007).
Os professores e investigadores matemáticos têm hoje presentes na Internet, materiais educativos disponíveis para o ensino da Matemática, entre eles, materiais didáticos como jogos educativos, e outros recursos a que podemos aceder e explorar diretamente on-line, (caso das applets, pequenos programas interativos que abordam tópicos específicos de Matemática) (Duarte, Portela & Torres, 2008).
O uso destas ferramentas permite que os alunos possam desenvolver o pensamento algébrico de uma forma mais dinâmica, não só na sala de aula, mas em qualquer momento, utilizando um computador com acesso à Internet. Em função do contato, praticamente diário, de muitos jovens com o computador, este tipo de abordagem tem também o potencial de cativar o interesse dos alunos que, por norma, são bastante recetivos às novidades, o que torna de suma importância a presença do professor como mediador da utilização destes recursos (Gandra, Aires & Catarino, 2016a).
Estes programas, que por vezes assumem a forma de jogos, são muitas vezes muito úteis para promover a aprendizagem de aspetos específicos da Álgebra (Ponte, Branco & Matos, 2009; Gandra, Aires & Catarino, 2016b). Os jogos matemáticos, desde que bem contextualizados, podem permitir, através do desenvolvimento do raciocínio, adquirir e assimilar conceitos em várias vertentes da Matemática.
Borin (1998) afirma que a introdução de jogos nas aulas de Matemática, onde é impossível a adoção de uma atitude passiva e a motivação é elevada, nota-se que os alunos apresentam um melhor desempenho e atitudes mais positivas frente ao seu processo de aprendizagem.
Sobre as potencialidades das applets no ensino e na aprendizagem da matemática, Figueiredo e Palha (2005) consideram que as applets têm um carácter interativo e que “a facilidade de compreensão destas applets que apelam fundamentalmente ao conhecimento informal dos alunos torna possível tratar os conceitos de uma forma natural e intuitiva, constituindo, desta forma, uma base sólida para um trabalho, posterior, mais formal.” (p. 7).
2. Relato da prática profissional
A experiência de ensino que apresentamos tem como foco a aprendizagem do cálculo das potências de base racional e expoente inteiro não negativo, e as regras das operações com potências, através da utilização das applets com formato de jogo.
Este episódio foi dinamizado no início do primeiro período do ano letivo de 2016/2017, durante uma aula de cinquenta minutos, numa turma da primeira autora, do 8.º ano de escolaridade, totalizando vinte e seis alunos, dezoito raparigas (69%) e oito rapazes (31%), com idades entre os 12 e 14 anos, sendo a média das idades de 12,97. Na avaliação final do ano anterior (7.º ano de escolaridade), quatro alunos obtiveram nível dois (15%) e os restantes alunos (85%) tiveram nível superior ou igual a três, numa escala de zero a cinco. No teste diagnóstico que decorreu na segunda aula deste ano letivo, vinte alunos (77%) apresentaram dificuldades no cálculo de potências de expoente natural e na aplicação das regras operatórias das potências.
O tema que estava a ser lecionado enquadrava-se no domínio da Álgebra, mais concretamente no tópico “potências de expoente inteiro” e tinha-se iniciado o subtema “potências de expoente inteiro negativo” com o cálculo de potências racionais de expoente inteiro negativo.
Durante os primeiros cinco minutos da aula, a professora dividiu a turma em grupos de seis e sete alunos e explicou que iriam ser aplicados dois jogos que permitiam trabalhar, por um lado, os conteúdos abordados nas aulas anteriores, isto é, as potências com expoente não negativo e regras operatórias e por outro lado, facilitavam a compreensão do subtema “Potências de expoente inteiro negativo” que seria lecionado nas próximas aulas.
Foram então utilizadas duas applets em formato de jogo durante trinta e cinco minutos. A todas as equipas (os grupos formados no início da aula) era solicitado que respondessem às questões que iam sendo formuladas e que justificassem a sua resposta. Se acertassem ganhavam os pontos estipulados na applet e se errassem, perdiam os pontos.
A primeira applet, Exponents Jeopardy Game (Figura 3), disponível em http://www.math-play.com/Exponents-Jeopardy/Exponents-Jeopardy.html, apresenta uma série de exercícios sobre potências que dizem respeito ao cálculo do valor de uma potência de expoente inteiro não negativo e indicação do expoente da potência.


Figura3- Exponents Jeopardy Game, site Math Play.
A segunda applet, Exponent Game with Kiwi (Figura 4), disponível em http://www.math-play.com/exponent-game.html, apresenta vários exercícios sobre as regras operatórias das potências.

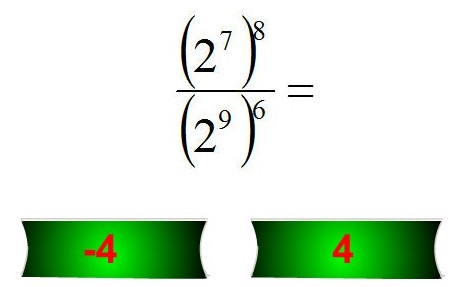 Figura4- Exponent Game with Kiwi, site Math Play.
Figura4- Exponent Game with Kiwi, site Math Play.
Na última parte da aula (10 minutos), sem qualquer ajuda, os alunos resolveram uma questão aula (QA) que constou da resolução de exercícios que visavam o cálculo das potências (Figura 5). Foi pedido aos alunos que a resolvessem individualmente e que registassem tudo o que faziam, que nunca apagassem o que tinham escrito e que, quando se enganassem, passassem um traço por cima e continuassem a resolução.
 Figura5- Questão Aula (QA) – Potências.
Figura5- Questão Aula (QA) – Potências.
Os dados foram recolhidos pela primeira autora que era a professora da turma, fazendo uso das técnicas seguintes: observação presencial; recolha de elementos escritos produzidos pelos alunos no âmbito das atividades individuais, permitindo obter informação sobre os conhecimentos e capacidades dos alunos; realização de registos, o mais pormenorizado possível, imediatamente a seguir às aulas, com observações e impressões do modo como os alunos reagiram e se envolveram nas tarefas, além de alguns episódios significativos.
3. Discussão e avaliação da implementação da prática profissional
As applets com formato de jogo foram utilizadas como um recurso didático-pedagógico com o objetivo que os alunos pudessem aprender de forma dinâmica e em grupo e com a possibilidade, de acordo com Alves (2007), de fixar conceitos, excitar o raciocínio e descobrir novos conceitos. E de fato, esta atividade surtiu o efeito esperado quanto à motivação e à interação entre os alunos.
No desenvolvimento do trabalho na aula em contacto com as applets, os alunos acedem ao processo de generalização a partir do que fazem para calcular as potências e/ou as expressões com potências e do que debatem com os colegas da equipa, quando procuram ultrapassar alguma dificuldade. Apropriam-se progressivamente do conceito de potência e das regras operatórias das potências, para generalizar o processo de resolução formal e desenvolvendo o pensamento algébrico (NCTM, 2007; Ponte et al., 2009).
No primeiro item da QA os coeficientes de sucesso obtidos, foram globalmente satisfatórios e alguns superaram as expetativas. Na sua maioria, os alunos sabem fazer o cálculo de uma potência de expoente inteiro e todos os alunos (100%) respondem que um número elevado a zero é um. Na tabela 1 apresenta-se a taxa de sucesso, em percentagem, da realização do item 1.
Tabela 1- QA – Cálculo de potências (item 1).
|
Alíneas |
1.1. |
1.2. |
1.3. |
|
Taxa de sucesso (%) |
100% |
77% |
100% |
As respostas incorretas têm várias proveniências: erro na tabuada e/ou erro no sinal do expoente. A Figura 6 exemplifica os erros verificados na resolução da segunda alínea deste item.
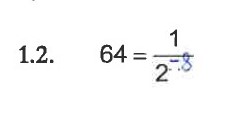
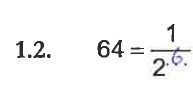
Figura6- Questão Aula (QA) – Exemplo de erros verificados no expoente da potência (item 1).
No item 2, todos os alunos (100%) reconhecem que na multiplicação de duas potências com a mesma base, adicionam-se os expoentes. A Figura 7 ilustra uma das respostas dadas pelos alunos.
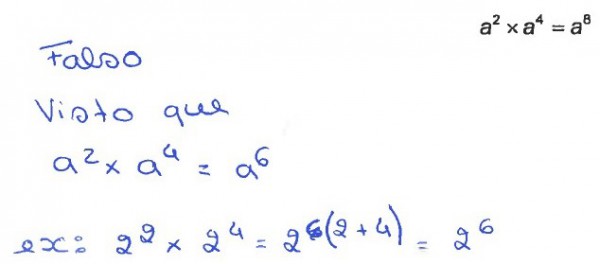 Figura7- Questão Aula (QA) – Exemplo de resposta (item 2).
Figura7- Questão Aula (QA) – Exemplo de resposta (item 2).
No item 3, os coeficientes de sucesso obtidos, foram satisfatórios. Na sua maioria, os alunos tem consciência das regras das operações com potências, mas cometem erros de natureza aritmética. Na tabela 2 apresenta-se a taxa de sucesso em percentagem da realização do item 3.
Tabela 2- QA – Regras operatórias das potências (item 1).
|
Alínea |
Taxa de sucesso (%) |
| 3.1 |
77% |
| 3.2 |
88% |
| 3.3 |
81% |
| 3.4 |
92% |
Os erros de natureza aritmética verificados nas alíneas do item 3, reportam-se às operações de adição, multiplicação e divisão de números racionais e/ou às regras de operações com potências. A Figura 8 ilustra um exemplo dos erros verificados.
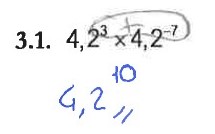
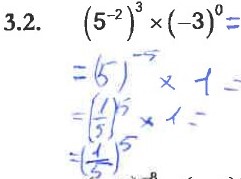
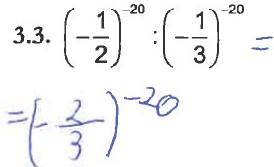
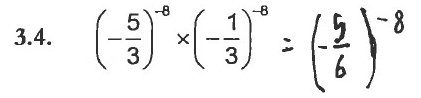
Figura 8- Questão Aula (QA) – Exemplo de erros verificados nas regras das potências (item 3).
Na aula seguinte à resolução da QA, a mesma foi entregue aos alunos corrigida. Durante a correção, que foi feita no quadro pelos alunos sob a orientação da professora, todos os erros detetados foram alvo de reflexão e diálogo com a turma. Ao verem a resolução correta dos itens, os alunos de viva voz, reconheceram que a precipitação e a falta de concentração contribuíram para os resultados obtidos e perceberam que necessitavam de estar mais atentos nas aulas. Alguns dos alunos (23%) reconheceram que tinham de fazer uma revisão às operações com números racionais.
Os resultados obtidos apontam para a confirmação da vantagem do uso das applets com formato de jogo no ensino e na aprendizagem das potências, desenvolvendo o pensamento algébrico dos alunos (Gandra, Aires & Catarino, 2016c). Recorrendo às applets torna-se simples observar diferentes casos, o que permite formular questões que levam a percorrer o caminho da descoberta e tornam a aprendizagem mais significativa, que é um dos objetivos das novas metas curriculares para o ensino básico (MEC, 2013).
Este estudo sugere que o professor se deve envolver diretamente na gestão curricular, selecionando recursos, estruturando e organizando tarefas que permitam envolver os alunos em atividades enriquecedoras. Sugere, também, que o uso das applets poderá contribuir para um melhor entendimento dos conceitos por parte dos alunos. É também importante referir que parece ter contribuído para o sucesso das aprendizagens retratado pelo facto da avaliação através da QA ter espelhado a participação dos alunos aquando a utilização das applets.
Ao refletir sobre a prática, esta experiência revelou-se muito gratificante, na medida em que contribui para um aprofundamento dos conhecimentos sobre as applets, bem como sobre as suas respetivas potencialidades no desenvolvimento do raciocínio matemático dos alunos.
Agradecimentos: Este trabalho foi financiado por Fundos Nacionais através da FCT – Fundação para a Ciência e a Tecnologia no âmbito do projeto UID/CED/00194/2013 e também do projeto UID/MAT/00013/2013.