1. Contexto da prática profissional

Muchas son las estrategias que actualmente se investigan en la búsqueda de un desarrollo integral de los estudiantes, es importante desenvolver estrategias diferenciadas que fomenten articulaciones entre el conocimiento matemático y las diferentes formas de representar ese conocimiento, así como, entre el saber académico y los conocimientos provenientes del cotidiano.

Desarrollamos un trabajo de investigación con alumnos del 11º año del área de artes de un instituto del noroeste de Portugal. El origen de todo el trabajo estuvo en la constatación de que estos alumnos no adquirieron conocimientos básicos de geometría que ya habían sido impartidos en el curso anterior. Los alumnos evidenciaron en las aulas de geometría descriptiva serias dificultades y obstáculos, en la comprensión de conceptos, en los procesos geométricos y en el desarrollo de un pensamiento argumentativo de carácter deductivo.

En una reunión intercalar los profesores de matemática y geometría descriptiva reflexionaron sobre este problema alertando al conjunto de los docentes de la clase para la importancia de los conceptos no interiorizados. Los profesores propusieron dos estrategias para colmatar las dificultades, por un lado, solicitar a la dirección del establecimiento un refuerzo en la carga horaria de los alumnos y por otro, que el profesor de matemática trabajase con los alumnos los conocimientos de geometría del año anterior. Por parte de la dirección de la escuela fue atribuido un tempo de 45 minutos a lo largo   de todo el curso y el profesor de matemática organizo el abordaje de los conceptos ya impartidos, con recurso a estrategias innovadoras, desarrollando procesos de enseñanza y aprendizaje que fuesen enriquecedores y estimulantes permitiendo el envolvimiento activo de los alumnos. Pretendemos analizar las dificultades de los alumnos de artes en adquirir conocimientos geométricos, así como, analizar los efectos de la implementación de estrategias creativas, en clase, dirigidas fundamentalmente para alumnos que evidencian dificultades en el ámbito de las matemáticas y así fomentar el envolvimiento activo, generando un proceso creativo, en los alumnos, que colabore en el desenvolvimiento de procesos de enseñanza y aprendizaje estimulantes.

Las dificultades de los alumnos en la interiorización y adquisición de conocimientos geométricos, en muchos casos, provienen, de la capacidad de abstracción que es exigida, principalmente en la visualización espacial y su representación. De ahí ser importante reflexionar sobre estrategias más adecuadas para tratar contenidos en el área de la geometría pues ésta desempeña un papel formativo como instrumento na interpretación e intervención sobre la realidad.

Los recursos didácticos pueden ayudar a desbloquear esas dificultades, las cuales son frecuentes en este dominio, por otro lado, la diversidad de recursos puede contribuir para la construcción de una metodología que se torne más eficaz junto del alumno. Esta eficacia pasa por favorecer el envolvimiento activo del alumno. (Aravena, Caamaño & Cabezas, 2007).

Según Pais (2006) la valoración de procedimientos de enseñanza más significativos requiere la superación de las prácticas reproductivas, sustituyéndolas por dinámicas que ayuden al alumno a desenvolver su creatividad, pues cada vez es más necesario fomentar la creatividad con miras a preparar a los alumnos, para enfrentar los retos contemporáneos.

La dinámica de la clase de matemática puede ser influenciada por factores muy diferentes, (Pires, 1999) enumera algunos de ellos destacando: el contexto escolar y social, los alumnos, con sus concepciones y aptitudes relativas a la matemática, así como sus conocimientos y experiencias; el profesor, con sus conocimientos y competencias profesionales, las actividades que éste propone y los materiales que los alumnos utilizan para su abordaje.

Diversas investigaciones (Alsina et-al., 1988; Fernández et-al, 1991; Calvo,1996) coinciden en que la geometría sirve para interpretar y actuar sobre el espacio, y que la utilización de materiales favorece la interacción del medio con el alumno y dan lugar a un aprendizaje más significativo.

La visualización es una forma de razonamiento en la investigación en matemáticas y, en particular, en Educación Matemática, es considerada importante, porque constituye una forma alternativa de acceder al conocimiento matemático; la comprensión de los conceptos matemáticos requiere múltiples representaciones y la representación visual puede transformar la comprensión de sí mismo; la visualización es parte de la actividad matemática. Es importante desarrollar en nuestros alumnos procesos fundamentales de las competencias geométricas, tales como   visualizar, manipular, explorar y modelar (Borba & Villarreal, 2005).

Al verificar que muchos de los conceptos subyacentes al capítulo geometría en el plano y el espacio, 10º ano de Matemática B, no habían sido adquiridos ni interiorizados reformulamos la planificación de los trabajos del 11º año teniendo como objetivo revisitar los conceptos geométricos ya impartidos, visto que, son fundamentales en el curso de artes ya que son utilizados con regularidad en otras de las asignaturas. Toda esta reformulación fue posible con la inclusión de un tiempo semanal de 45 minutos, a lo largo de todo el año escolar, lo que permitió trabajar con los alumnos los conceptos de geometría del año anterior.

Intentando dar cuenta del alcance pretendido desarrollamos un estudio de carácter cualitativo e interpretativo procurando analizar y comprender como la implementación de estrategias creativas puede fomentar el envolvimiento activo y generar un proceso creativo en los alumnos desenvolviendo, de esta forma, procesos de enseñanza y aprendizaje estimulantes.  Acompañamos todo el desarrollo del trabajo de los intervinientes, intentando comprender las motivaciones, necesidades y comportamientos de los elementos involucrados en la investigación, para tal pusimos en práctica un estudio de caso. La clase involucrada es la del 11º Año del área de artes, formada por siete alumnos en la asignatura de Matemática B, con edades comprendidas entre los 15 y los 20 años. Los alumnos de esta clase evidenciaban grandes dificultades en la interpretación y aplicación de los conceptos impartidos en el 10º año.  Dos de estos alumnos están por tercera vez en el 11º año. Por lo general son alumnos con muchas dificultades en todas las asignaturas a lo que no escapa la matemática, pero la mayoría se muestran interesados y van desenvolviendo sus capacidades, cuando tomamos como referencia el punto donde se iniciaron.

Introducimos artefactos de otra cultura en clase, con dos objetivos, fomentar el envolvimiento activo de los estudiantes trabajando en clase la cestería de otro país, República Democrática de Timor Este e iniciar el abordaje a los conceptos de geometría del 10º año que no estaban adquiridos. Al introducir en la clase artefactos ajenos a la realidad cultural de los alumnos, es posible que éstos se evidencien como entes motivadores y facilitadores de la interiorización de conceptos matemáticos.

Se pretendió que los alumnos analizasen  artefactos de cestería bajo el  punto de vista de los modelos o  patrones  geométricos solicitamos a los alumnos la identificación de algunos elementos, transformaciones geométricas, frisos o pavimentaciones, que pudiesen estar presentes en la construcción de los artefactos en análisis y, por otro lado, como los artefactos estudiados proceden de Timor Este, también se  pretendía fomentar en los alumnos una estima por la diversidad cultural y desenvolver el  gusto por el conocimiento de otras culturas. El trabajo se desenvolvió a lo largo de 7 clases con la duración de 90 minutos cada una.  Durante todo el trabajo se grabaron en audio las clases y se procedió a la filmación de algunas de ellas. Los alumnos construyeron los respectivos informes acompañados de los trabajos desarrollados en las diferentes aulas.

Nuestro trabajo se centró en analizar las dificultades subyacentes al aprendizaje de conceptos geométricos y por otro lado valorar el efecto que puede producir la inclusión en la clase de artefactos de otra cultura como elementos catalizadores del aprendizaje. Pretendemos analizar las dificultades de los alumnos de artes en adquirir conocimientos geométricos, así como, analizar los efectos de la implementación de estrategias creativas, en clase, dirigidas fundamentalmente para alumnos que evidencian dificultades en el ámbito de las matemáticas y así fomentar el envolvimiento activo, generando un proceso creativo, en los alumnos, que colabore en el desenvolvimiento de procesos de enseñanza y aprendizaje estimulantes.

1. Relato da prática profissional

Iniciamos el desenvolvimiento del trabajo, en clase, con la formación de 2 grupos de trabajo Grupo A: Tiago; Rita; Bruna; Melissa; Grupo B: Daniela; Bianca; Tatiana (nombres ficticios). A cada uno de los grupos les fueron fornecidos dos cestos y un guion para el desenvolvimiento del trabajo. A continuación, presentamos la traducción del guion proporcionado a los alumnos:

Al solicitar a los alumnos que dibujasen de forma libre los artefactos pretendimos ir al encuentro de sus gustos, visto tratarse de una clase de artes, por otro lado, al registrar en papel milimetrado tuvimos como objetivo desenvolver la capacidad de observación y análisis de la realidad y facilitar la interpretación de los conceptos matemáticos subyacentes a la construcción de los artefactos.

En la figura 1 y 2 observamos los artefactos distribuidos a cada grupo. Solicitamos que, puntualmente, usasen sus móviles para fotografiar los objetos. A continuación, se les explicó que procedían de Timor Este y solicitamos su participación en el sentido de que hablasen sobre lo que conocían de un país tan lejano. Refirieron que tenían alguna idea, pero no muy clara de su posición geográfica, así como de la relación histórica con Portugal. Se aprovechó este momento para de forma resumida referenciar la relación histórica de Timor Este con Portugal y solicitar a los dos grupos que, en casa, hicieran una pesquisa sobre Timor Este, su historia y cestería.

Figura1- Cestos fornecidos ao grupo A

Figura2-  Cestos fornecidos ao grupo B

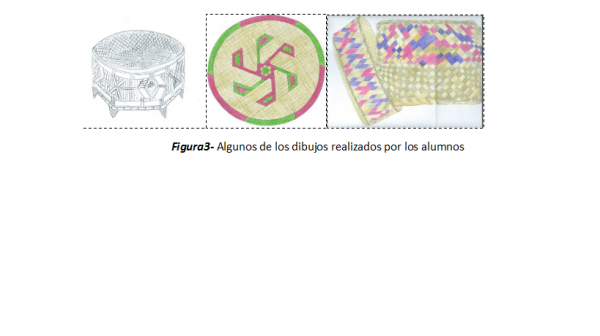
La primera parte del trabajo consistió en solicitar a los alumnos que dibujasen los artefactos, destacando que cada elemento del grupo debería hacer un dibujo de uno de los cestos. La primera pregunta por parte de los alumnos fue si había necesidad de rigor a lo que se contestó, en el sentido de hacerles ver que en esta primera fase y como alumnos de arte, podían hacer una interpretación libre de la realidad, dibujando el artefacto conforme su sentido artístico y su intuición, en la figura 3 presentamos algunas de las representaciones realizadas por los alumnos.

Figura3- Algunos de los dibujos realizados por los alumnos           

En el tercero y cuarto período de 90 minutos se les entregó papel milimetrado y hablamos sobre esta nueva fase del trabajo, donde ahora no es la visión del artista, pero si la visión del investigador matemático que pretende descubrir que patrones geométricos existen en los artefactos. Entonces procedieron a la representación, en el papel proporcionado, de las partes que consideraban más importantes de los artefactos.

En el quinto y sexto período de 90 minutos utilizaron sus representaciones para identificar patrones geométricos y transformaciones geométricas. Por último, fue indicado que deberían elaborar un informe, y posteriormente a su lectura y análisis, por parte de la profesora, tenían que hacer la presentación, reflexión y discusión sobre el trabajo desarrollado.

En el séptimo período de 90 minutos, cada grupo de trabajo, con recurso a una presentación en power point, expuso su trabajo. Cada grupo tuvo 15 minutos para su exposición y posteriormente discutimos aspectos importantes relacionados con los conceptos matemáticos subyacentes al desenvolvimiento del trabajo y las dificultades que quedaron evidentes en las exposiciones, así como las que ya habían sido identificadas en el análisis de los informes.

A continuación, mostramos algunos de los trabajos desarrollados por los alumnos donde quedaron patentes las dificultades para interpretar la realidad y explicarla con un cierto rigor.

Situación 1: Pavimentaciones

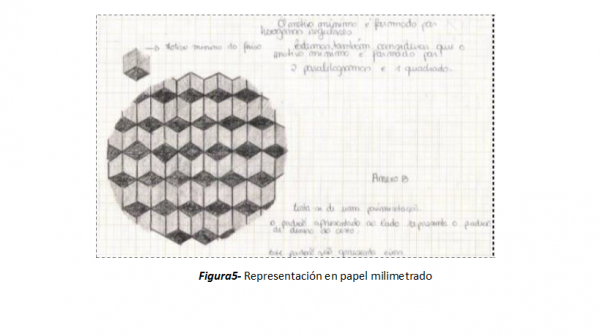
En la figura 4 presentamos el registro fotográfico de uno de los cestos desde dos ángulos diferentes de visión y en la figura 5, la representación de la base del mismo cesto en papel milimetrado por parte de uno de los alumnos.

Figura4- Parte superior de uno de los cestos

Figura5- Representación en papel milimetrado

Observamos que la alumna no comprende la diferencia entre friso y pavimentación, cuando identifica que está en presencia de una pavimentación y al mismo tiempo identifica el motivo mínimo del friso. Por otro lado, refiere el motivo mínimo como un hexágono regular, y gráficamente identifica un cubo. En la discusión oral del trabajo se le pidió a la alumna que construyese una pequeña parte de la pavimentación. Procedió a la construcción usando un cubo y se generó la discusión sobre la definición que habían presentado, donde indicaban que la pavimentación era construida con polígonos. Toda esta discusión permitió clarificar con los alumnos ideas importantes sobre el plano y el espacio, fomentando el desarrollo de las capacidades de visualización, reconocimiento, identificación, clasificación y representación de relaciones geométricas.

Situación 2: Frisos

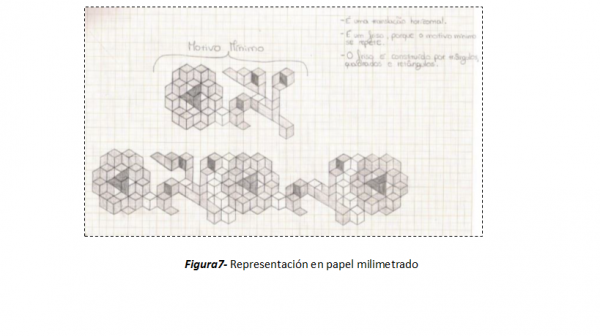
En la figura 6 observamos el registro fotográfico de uno de los cestos con dos perspectivas diferentes y en la figura 7 la representación del detalle ornamental del cesto en papel milimetrado.

Figura6- Detalle lateral de uno de los cestos

Figura7- Representación en papel milimetrado

Observamos dificultades en la identificación de las transformaciones que están subyacentes a la construcción del friso, la identificación del friso según esta alumna proviene de la repetición de un motivo e refiere una translación horizontal. En la discusión oral solicitamos que hiciese en el encerado el friso usando solamente una translación, le obligamos a escoger un vector para asociar a la translación y ella misma verificó que existían otras transformaciones asociadas para que la construcción del friso fuese la deseada. La alumna dijo “necesito de algo más para que dé la vuelta”, habiendo discutido entonces como son formados los frisos y cuales las transformaciones inherentes a su construcción. A continuación, proyectamos la fotografía del cesto y verificamos que no existía la necesidad de “dar la vuelta”; fue esta alumna quien en su representación construyó un friso diferente del que había en el artefacto.

1. Discussão e avaliação da implementação da prática profissional

A lo largo del estudio desarrollado verificamos que uno de los puntos fuertes de este trabajo fue la receptividad con la que los alumnos lo encararon. Los artefactos introducidos funcionaron como elementos motivadores y dinamizadores, así como, también permitieron transponer los aprendizajes para contextos fuera de las matemáticas y fomentaron momentos de reflexión y crítica social colaborando en la formación de individuos críticos y reflexivos ante la realidad que los rodea.

A lo largo de toda la construcción surgieron momentos en los que quedaron evidentes las dificultades de estos alumnos; cuando pretendían representar las figuras geométricas, lo que verificamos al acompañar el trabajo de cada grupo. Uno de los problemas que quedó patente en casi todos fue que cuando pretendían representar un cuadrado y su diagonal, asumían que las medidas eran iguales y cuando repetían el patrón decían “no cuadra”. Se dibujó en el encerado un cuadrado de lado uno y se les pidió que calculasen la medida de la diagonal. Lo fueron haciendo y comprendieron que las medidas eran diferentes, lo que permitió que identificasen el problema subyacente a su “no cuadra”.

Durante la discusión final de los informes, muchos de los conceptos subyacentes al desenvolvimiento del trabajo fueron nuevamente abordados al poner de manifiesto la falta de rigor y la no consecución de los objetivos establecidos. Verificamos que los alumnos no consiguen formalizar los conceptos adquiridos y que, en la mayoría de los casos, las nociones geométricas son expresadas de forma intuitiva, sin la formalización y el rigor que deberían estar asociados a este nivel de estudios. También evidenciaron una gran dificultad en expresar sus ideas en la discusión oral, así como, en la capacidad de abstracción que es exigida, principalmente en la visualización espacial y su representación.

Observamos, tal como refieren Aravena, Caamaño & Cabezas (2007) que los alumnos presentan serias dificultades y obstáculos, tanto en la comprensión de los conceptos, como en los procesos geométricos y en el desarrollo de un pensamiento argumentativo de carácter deductivo, lo que dificulta el desarrollo de procesos de pensamiento y razonamiento matemático.

Al analizar los resultados académicos de estos alumnos verificamos que existió una leve mejoría en la aplicación de los conceptos geométricos abordados y que en el examen nacional las preguntas de geometría fueron unas en las que tuvieron un relativo suceso y se observó una mejoría en Geometría Descriptiva y también en la asignatura de Diseño, fundamentalmente en los trabajos que envolvían conceptos de carácter geométrico. No en tanto, los resultados no son todo lo satisfactorio que pretendíamos, algunos de ellos continuaron a evidenciar dificultades en la aplicación y comprensión de conceptos geométricos básicos.

Aunque a nivel de los conceptos geométricos, subyacentes al desenvolvimiento del trabajo, éste no haya dado los frutos deseados, de nuestra parte consideramos que fue positivo en el sentido de contribuir para una mayor receptividad por parte de los alumnos a la geometría, así como colaborar en la construcción del conocimiento de una forma sustentada.

Nuestros resultados coinciden con las investigaciones (Alsina et-al., 1988; Fernández et-al., 1991; Calvo, 1996) en el sentido de que la utilización de materiales favorece la interacción del medio con el alumno y da lugar a un aprendizaje más significativo. Los artefactos introducidos en clase se evidenciaron como elementos motivadores e facilitadores del aprendizaje, permitiendo que el revisitar de los conceptos ya impartidos, se realizase con entusiasmo y motivación.

En el desarrollo del estudio quedaron patente las dificultades que estos alumnos tienen en la formalización e interiorización de los conceptos geométricos, pero la inclusión en clase de recursos educativos innovadores y fomentadores de la creatividad se reveló como un catalizador de los procesos de enseñanza y aprendizaje. Los alumnos mejoraron sus resultados en la utilización y aplicación de conceptos geométricos tanto en la disciplina de matemática como en la de geometría descriptiva.

Este trabajo pone en evidencia que la integración en la clase de formas de trabajo matemático de naturaleza más abierta, puede funcionar como elemento motivador, fomentar la creatividad y el gusto por descubrir y saber hacer, contribuyendo para la mejoría de los resultados académicos de nuestros alumnos.